【LeetCode-Aug】-Aet

Bingliaolong 2024-08-10 15:34 Aet | 隐藏边栏 | 抢沙发 | 28 0

文章评分 3 次，平均分 5.0 ：

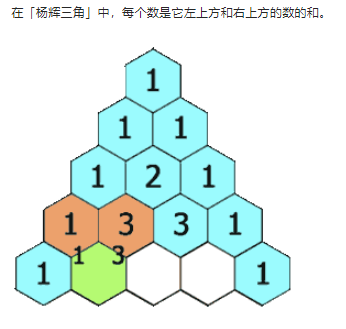
118 杨辉三角

Question

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行

Pic

Case

示例一：

1 2	输入: numRows = 5 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

实例二：

1 2	输入: numRows = 1 输出: [[1]]

Tips

1 <= numRows <= 30

Ans1

初始版本

class Solution {

public:

vector<vector<int>> generate(int numRows) {

assert(numRows != 0);

vector<int> first = {0, 1, 0};

vector<vector<int>> res;

if (numRows > 1) {

for (auto tmp_size = 0; tmp_size < numRows; tmp_size++) {

if (tmp_size == 0) {

res.push_back({1});

} else {

vector<int> vec_tmp;

for(size_t sz = 0; sz < first.size() - 1; sz++) {

vec_tmp.push_back(first[sz]+first[sz+1]);

}

first.clear();

first.push_back(0);

first.insert(first.end(), vec_tmp.begin(), vec_tmp.end());

first.push_back(0);

res.push_back(vec_tmp);

}

} else {

res.push_back({1});

}

return res;

}

};

Ans2

优化版本

class Solution {

public:

vector<vector<int>> generate(int numRows) {

vector<vector<int>> res;

if (numRows >= 1) {

res.push_back({1});

}

for (int i = 1; i < numRows; i++) {

vector<int> row(i+1, 1);

for (int j = 1; j < i; j++) {

row[j] = res[i-1][j-1] + res[i-1][j];

}

res.push_back(row);

}

return res;

}

};

解析：
if (numRows >= 1) {res.push_back({1});}
1. 不管有一层还是多层，第一层都是一样的，都是{1}
for (int i = 1; i < numRows; i++) {
1. 这个循环，其实就是从第二层开始构建杨辉三角，numRows是多少，就需要构建多少层杨辉三角
2. 而之所以从第二层（下标为1）的开始，是因为第一层通过if(numRows>=1){res.push_back({1});}这段代码已经构建好了
vector<int> row(i+1, 1);
1. 根据已知的规律（n层的杨辉三角，第1层1个元素，第2层2个元素，第n层有n个元素）来创建每一层用于存放杨辉三角的数据的容器的大小
2. 并全部初始化为1（只所以这样做，是因为没一层的第一个和最后一个必然是1，这样全部初始化为1，只需要从每一层的第2个元素即下标为1的元素重新计算）
for (int j = 1; j < i; j++) {
1. 这个循环，对于每一层，从第2个元素开始重新计算它的值
  因为我们初始化的时候已经设置了正确的每一层的第一个以及最后一个元素
2. 而第二个元素的下标为1，所以j从等于1开始
3. j之所以需要小于i，对于每一层而言，下标的最大值就是i的值，所以当要用表示下标的j来处理元素，无论如何，j也不可以大于每一层的下标的最大值i
4. 至于为什么不能等于下标i（最大值），因为最大值i表示了每一层的最后一个元素，而最后一个元素，我们在初始化的时候，已经赋予了它正确的值，所以不需要处理
row[j] = res[i-1][j-1] + res[i-1][j];
1. 因此，能执行这一行代码的情况，一定是在第一个元素和最后一个元素中间，还有元素的层
2. 不满足这样的条件的层，不会执行这行代码，所以，对于{1,1}这样的情况（也就是第二层），自然无须担心

9 回文数

Question

给你一个整数 x ，如果 x 是一个回文整数，返回 true ；否则，返回 false
回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数

Case

示例 1：

1 2	输入：x = 121 输出：true

示例 2：

输入：`x = -121`

输出：`false`

解释：从左向右读, 为 `-121` 。从右向左读, 为 `121-` 。因此它不是一个回文数

示例 3：

输入：`x = 10`

输出：`false`

解释：从右向左读, 为 `01` 。因此它不是一个回文数

示例4：

1 2	负数不是回文数 0-9的数是回文数

Tips

Ans1

初始版本

class Solution {

public:

bool isPalindrome(int x) {

if (x >= 0 && x < 10) {

return true;

} else if (x < 0) {

return false;

}

std::vector<int> tmp;

int tx = x;

while (tx != 0) {

auto ttx = tx;

tx /= 10;

tmp.push_back(ttx % 10);

}

bool res = true;

auto size = tmp.size();

for (size_t i = 0; i < size / 2; i++) {

if (tmp[i] != tmp[size - i - 1]) {

res = false;

}

return res;

}

};

Ans2

优化版本

class Solution {

public:

bool isPalindrome(int x) {

// 特殊情况处理

if (x < 0 || (x % 10 == 0 && x != 0)) {

return false;

}

int revertedNumber = 0;

while (x > revertedNumber) {

revertedNumber = revertedNumber * 10 + x % 10;

x /= 10;

}

// 当原数是奇数位时，revertedNumber 可能比 x 多一位，需要除以 10 去掉中间位

return x == revertedNumber || x == revertedNumber / 10;

}

};

解析
1. 利用原数进行构建反转数，但只构建一半
2. 构建循环的退出条件是构建的反转数等于或大于原数剩余的部分时，退出构建
3. 然后进行判断，如果构建的反转数与原数的剩余部分相等，则是回文数
  不想等的情况，是构建的反转数比原数的剩余部分多一位
4. 所以对构建的反转数进行一次以10取整，来判断是否相等，相等则为回文数，否则不是

13 罗马数字

Question

罗马数字包含以下七种字符: I， V， X， L，C，D 和 M

I 1

V 5

X 10

L 50

C 100

D 500

M 1000

例如，罗马数字 2 写做 II ，即为两个并列的 1 。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II

Case

示例1

1 2	输入: s = "III" 输出: 3

示例2

1 2	输入: s = "IV" 输出: 4

示例3

1 2	输入: s = "IX" 输出: 9

示例4

输入: s = "LVIII"

输出: 58

解释: L = 50, V= 5, III = 3

示例5

输入: s = "MCMXCIV"

输出: 1994

解释: M = 1000, CM = 900, XC = 90, IV = 4

Tips

通常情况下，罗马数字中小的数字在大的数字的右边
1. 但也存在特例，例如 4 不写做 IIII，而是 IV
2. 数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4
3. 同样地，数字 9 表示为 IX
这个特殊的规则只适用于以下六种情况：
1. I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9
2. X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。
3. C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900

Ans

class Solution {

public:

int romanToInt(string s) {

static const std::unordered_map<char, int> mp = {

{'I', 1},

{'V', 5},

{'X', 10},

{'L', 50},

{'C', 100},

{'D', 500},

{'M', 1000}

};

int res = 0;

for (int i = 0; i < s.size(); i++) {

int cur_val = mp.at(s[i]);

if (i + 1 < s.size() && mp.at(s[i+1]) > cur_val) {

res -= cur_val;

} else {

res += cur_val;

}

return res;

}

};

14 最长公共前缀

Question

编写一个函数来查找字符串数组中的最长公共前缀
如果不存在公共前缀，返回空字符串 ""

Case

示例1

1 2	输入：strs = ["flower","flow","flight"] 输出："fl"

示例2

输入：strs = ["dog","racecar","car"]

输出：""

解释：输入不存在公共前缀

Tips

1 <= strs.length <= 200
0 <= strs[i].length <= 200
strs[i] 仅由小写英文字母组成

Ans

class Solution {

public:

string longestCommonPrefix(vector<string>& strs) {

if(strs.empty()) { return ""; }

string res;

for (size_t i = 0; i < strs[0].size(); i++) {

for (size_t j = 1; j < strs.size(); j++) {

if (i >= strs[j].size() || strs[j][i] != strs[0][i]) {

return res;

}

res += strs[0][i];

}

return res;

}

};

58 最后一个单词的长度

Question

给你一个字符串 s，由若干单词组成，单词前后用一些空格字符隔开。返回字符串中最后一个单词的长度
单词是指仅由字母组成、不包含任何空格字符的最大子字符串

Case

示例1

输入：s = "Hello World"

输出：5

解释：最后一个单词是“World”，长度为 5

示例2

输入：s = " fly me to the moon "

输出：4

解释：最后一个单词是“moon”，长度为 4

示例3

输入：s = "luffy is still joyboy"

输出：6

解释：最后一个单词是长度为 6 的“joyboy”

Ans1

class Solution {

public:

int lengthOfLastWord(string s) {

int length = 0;

bool flag = false;

for (auto ite = s.rbegin(); ite != s.rend(); ite++) {

if (*ite != ' ') {

flag = true;

length++;

} else {

if (flag) {

break;

}

return length;

}

};

Ans2

class Solution {

public:

int lengthOfLastWord(string s) {

int length = 0;

// 使用反向迭代器从后向前遍历字符串

for (auto ite = s.rbegin(); ite != s.rend(); ++ite) {

if (*ite != ' ') {

length++;

} else if (length > 0) { // 如果已经开始计数并遇到空格，则结束

break;

}

return length;

}

};

66 加一

Question

给定一个由整数组成的非空数组所表示的非负整数，在该数的基础上加一
最高位数字存放在数组的首位，数组中每个元素只存储单个数字
你可以假设除了整数 0 之外，这个整数不会以零开头

Case

示例1

输入：digits = [1,2,3]

输出：[1,2,4]

解释：输入数组表示数字 123

示例2

输入：digits = [4,3,2,1]

输出：[4,3,2,2]

解释：输入数组表示数字 4321

示例3

1 2	输入：digits = [0] 输出：[1]

Ans1

初始

class Solution {

public:

vector<int> plusOne(vector<int>& digits) {

if (digits.size() == 1) {

if (digits[0] + 1 < 10) {

digits[0]++;

} else {

digits[0] = 0;

digits.insert(digits.begin(), 1);

}

return digits;

}

auto index = digits.size() - 1;

bool flag = false;

while (index > 0) {

if (flag) {

if (digits[index] < 10) {

break;

} else {

digits[index] = 0;

digits[index-1]++;

index--;

continue;

}

if (digits[index] + 1 < 10) {

digits[index]++;

break;

} else {

flag = true;

digits[index] = 0;

digits[index-1]++;;

index--;

}

if (digits[0] >= 10) {

digits[0] = 0;

digits.insert(digits.begin(), 1);

}

return digits;

}

};

Ans2

优化

class Solution {

public:

vector<int> plusOne(vector<int>& digits) {

int n = digits.size();

for (int i = n - 1; i >= 0; i--) {

if (digits[i] < 9) {

digits[i]++;

return digits;

}

digits[i] = 0;

}

digits.insert(digits.begin(), 1);

return digits;

}

};

67 二进制求和

Question

给你两个二进制字符串 a 和 b ，以二进制字符串的形式返回它们的和

Case

示例1

1 2	输入:a = "11", b = "1" 输出："100"

示例2

1 2	输入：a = "1010", b = "1011" 输出："10101"

Tips

1 <= a.length, b.length <= 104
a 和 b 仅由字符 '0' 或 '1' 组成
字符串如果不是 "0" ，就不含前导零

Ans

常规的思路不可行：
1. 用bitset将a和b转成int（不是直接把streing转成int），再将相加后得到的int转成bitset，利用bitset的to_string得到二进制字符串
2. 然后从左向右，使用string得find找到第一个不为0的位，再使用substr从该位向后截取
3. 对于常规的一些case来讲，该思路实现的方法是可以满足效果的
4. 但是对于超级长的二进制字符串，bitset的to_ulong会截断处理，因此该方法不能正确处理大数
下面的方法是针对字符串进行处理

class Solution {

public:

string addBinary(string a, string b) {

string result = "";

int carry = 0;

int i = a.size() - 1;

int j = b.size() - 1;

while (i >= 0 || j >= 0 || carry) {

int sum = carry;

if (i >= 0) {

sum += a[i--] - '0';

}

if (j >= 0) {

sum += b[j--] - '0';

}

result += (sum % 2) + '0';

carry = sum / 2;

}

reverse(result.begin(), result.end());

return result;

}

};

解析：
1. int carry = 0;
2. 用于存储每一位相加后的进位
3. int i = a.size() - 1;
4. int j = b.size() - 1;
5. 从两个字符串的末位开始处理
6. while (i >= 0 || j >= 0 || carry) {
7. ij表示索引，那它当然要大于等于0，不管是长的字符串还是短的字符串，每一位都要处理
  同时carry保存的是进位，也需要处理
8. int sum = carry;
9. 临时的计算和
10. if (i >= 0) {
11. 由于ij在使用后会自减，所以循环中在使用前，需要对它进行判断，作为下标索引，它得大于等于0
12. sum += a[i--] - '0';
13. 首先是用字符减去字符0，利用ASCII编码的特点，将字符转成int值
  然后把值保存到sum里面，同理，字符串b也需要进行同样的操作，都从最后一位开始
14. res += (sum % 2) + '0';
15. sum是两个字符串从末位对齐后，按末位相加的结果，之所以是%2，是因为事先知道目标元素是二进制1和0的字符相加所得到的结果，所以通过%2对相加结果进行取余，得到该位计算后最终的值
16. 之后加上字符‘0’，是想把结果从int值转成ASCII字符
17. carry=sum/2；
18. 获得两同位字符按数字相加后在二进制规则下的进位量

125 验证回文串

Question

如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后，短语正着读和反着读都一样。则可以认为该短语是一个回文串
字母和数字都属于字母数字字符
给你一个字符串 s，如果它是回文串，返回 true ；否则，返回 false

Case

示例1

输入: s = "A man, a plan, a canal: Panama"

输出：true

解释："amanaplanacanalpanama" 是回文串。

示例2

输入：s = "race a car"

输出：false

解释："raceacar" 不是回文串。

示例3

输入：s = " "

输出：true

解释：在移除非字母数字字符之后，s 是一个空字符串 "" 。

由于空字符串正着反着读都一样，所以是回文串。

Tips

Ans1

class Solution {

public:

bool isPalindrome(string s) {

string temp;

for (auto c : s) {

if (std::isalpha(c)) {

temp += c | 0x20;

} else if (std::isdigit(c)) {

temp += c;

}

if (temp.size() == 0) {

return true;

}

string rev;

size_t index = temp.size() - 1;

while (index + 1 > rev.size()) {

rev += temp[index--];

}

temp = temp.substr(0, index + 1);

if (rev.compare(temp) == 0) {

return true;

} else {

rev = rev.substr(0, rev.size() - 1);

return (rev.compare(temp) == 0);

}

};

Ans2

优化版

class Solution {

public:

bool isPalindrome(string s) {

int left = 0;

int right = s.size() - 1;

while (left < right) {

while (left < right && !std::isalnum(s[left])) {

left++;

}

while (left < right && !std::isalnum(s[right])) {

right--;

}

if ((s[left] | 0x20) != (s[right] | 0x20)) {

return false;

}

left++;

right--;

}

return true;

}

};

242 有效的字母异位词

Question

Case

Ans1

map 是一个有序容器，插入和查找操作的时间复杂度为 O(log n)
对于这个问题，使用无序容器 unordered_map 更合适，插入和查找的时间复杂度为 O(1)，这将提高性能
代码中，先比较了 map 的大小，然后再逐一比较其中的元素
这种情况下，可以在第二次遍历时直接查找和比较，而不需要额外的大小检查
因为字符范围已知（小写字母 a-z），可以直接使用一个大小为 26 的数组来统计每个字符的出现次数
这会减少内存开销并提高查找效率

class Solution {

public:

bool isAnagram(string s, string t) {

map<int,int> mps, mpt;

for (auto c : s) {

mps[c - 'a']++;

}

for (auto c : t) {

mpt[c - 'a']++;

}

if (mps.size() != mpt.size()) {

return false;

}

for (auto ite : mps) {

if (mpt[ite.first] != ite.second) {

return false;

}

return true;

}

};

Ans2

优化

class Solution {

public:

bool isAnagram(string s, string t) {

if (s.size() != t.size()) {

return false;

}

int count[26] = {0};

for (auto c : s) {

count[c - 'a']++;

}

for (auto c : t) {

count[c - 'a']--;

if (count[c - 'a'] < 0) {

return false;

}

return true;

}

};

383 赎金信

Question

给你两个字符串：ransomNote 和 magazine ，判断 ransomNote 能不能由 magazine 里面的字符构成
如果可以，返回 true ；否则返回 false
magazine 中的每个字符只能在 ransomNote 中使用一次

Case

示例1

1 2	输入：ransomNote = "a", magazine = "b" 输出：false

示例2

1 2	输入：ransomNote = "aa", magazine = "ab" 输出：false

示例3

1 2	输入：ransomNote = "aa", magazine = "aab" 输出：true

Ans

class Solution {

public:

bool canConstruct(string ransomNote, string magazine) {

int count[26] = {0};

for (auto c : magazine) {

count[c - 'a']++;

}

for (auto c : ransomNote) {

count[c - 'a']--;

if (count[c - 'a'] < 0) {

return false;

}

return true;

}

};

387 字符串中的第一个唯一字符

Question

给定一个字符串 s ，找到 它的第一个不重复的字符，并返回它的索引 。如果不存在，则返回 -1

Case

示例1

1 2	输入: s = "leetcode" 输出: 0

示例2

1 2	输入: s = "loveleetcode" 输出: 2

示例3

1 2	输入: s = "aabb" 输出: -1

Tips

1 <= s.length <= 105
s 只包含小写字母

Ans1

想法是用pos这个数组来记录所有字符第一次出现的索引
1. 将pos初始化为-1，因为作为索引，是需要大于等于0
遍历字符串的每个字符，按照字符的ASCII值，在数组中下标为该值的位置记录下索引的值
1. 记录的时候，如果该值为-1，表面第一次记录，于是更新成正确的索引值，此时它是大于等于0的
2. 然后，对于再次循环时，该位置大于等于0的值再次处理，说明该外置的字符已经处理过了，是第二次次遇到了
3. 于是把该外置的值更新为-2，表示该值是重复的，而后续对于第二次出现过的字符，已经不需要再处理了，跳过
这样，循环完，pos里面有3种值，-1，-2，大于等于0的
1. 首先找打第一个大于等于0的，作为初始最小索引
2. 然后遍历该数组，找到所有大于等于的索引里面最小索引
3. 就是最早出现的唯一字符

class Solution {

public:

int firstUniqChar(string s) {

std::array<int, 26> pos;

pos.fill(-1);

for (size_t i = 0; i < s.size(); i++) {

auto index = s[i] - 'a';

if (pos[index] == -2) {

continue;

} else if (pos[index] == -1) {

pos[index] = static_cast<int>(i);

} else {

pos[index] = -2;

}

int min = -1;

for (int i = 0; i < 26; i++) {

if (pos[i] >= 0) {

if (min < 0) {

min = pos[i];

} else if (pos[i] < min) {

min = pos[i];

}

return min;

}

};

Ans2

优化

class Solution {

public:

int firstUniqChar(string s) {

int pos[26] = {0};

for (auto c : s) {

pos[c - 'a']++;

}

for (int i = 0; i < s.size(); i++) {

if (pos[s[i] - 'a'] == 1) {

return i;

}

return -1;

}

};

389 找不同

Question

给定两个字符串 s 和 t ，它们只包含小写字母
字符串 t 由字符串 s 随机重排，然后在随机位置添加一个字母
请找出在 t 中被添加的字母

Case

示例1

输入：s = "abcd", t = "abcde"

输出："e"

解释：'e' 是那个被添加的字母

示例2

1 2	入：s = "", t = "y" 输出："y"

Tips

0 <= s.length <= 1000
t.length == s.length + 1
s 和 t 只包含小写字母

Ans1

class Solution {

public:

char findTheDifference(string s, string t) {

int count[26] = {0};

for (auto c : t) {

count[c - 'a']++;

}

for(auto c : s) {

count[c - 'a']--;

}

for (int i = 0; i < 26; i++) {

if (count[i] == 1) {

return i + 'a';

}

return 'a';

}

};

Ans2

非优化，方案2

class Solution {

public:

char findTheDifference(string s, string t) {

char res = 0;

for (auto c : s) {

res ^= c;

}

for (auto c : t) {

res ^= c;

}

return res;

}

};

392 判断子序列

Question

给定字符串 s 和 t ，判断 s 是否为 t 的子序列
字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串
（例如，"ace"是"abcde"的一个子序列，而"aec"不是）
进阶：
1. 如果有大量输入的 S，称作 S1, S2, ... , Sk 其中 k >= 10亿，你需要依次检查它们是否为 T 的子序列
  在这种情况下，你会怎样改变代码？

Case

示例1

1 2	输入：s = "abc", t = "ahbgdc" 输出：true

示例2

1 2	输入：s = "axc", t = "ahbgdc" 输出：false

Ans1

class Solution {

public:

bool isSubsequence(string s, string t) {

int index = 0;

for (auto c : t) {

if (index < s.size() && s[index] == c) {

index++;

}

return (index == s.size());

}

};

Ans2

另一种思路
1. 先把t的每一个元素的所有索引用vector<vector<int>> vec_indexs保存下来
2. 遍历s的每一个字符c，用c到vec_indexs里面获取同字符的索引vector<int> vec
3. 设置一个要查找的索引prev_index，初始化为-1，从vec里面查找有没有大于-1也就是prev_index的索引
4. 查找使用二分查找auto ite = std::upper_bound(vec.begin(), vec.end(), prev_index);
5. 如果找不到，那说明s的第一个字符在t里面都找不到，肯定不是t的子串，返回false
6. 如果找到了，需要更新prev_index，而下一个字符的索引一定是要比前一个字符出现的最小索引要大的
7. 所以把prev_index更新为*ite
8. 循环到下一次时，要查的是下一个字符，而下一个字符的索引要大于prev_index
9. 循环完成后，说明s的每一个字符都在t中按顺序找到了，返回true

class Solution {

public:

bool isSubsequence(string s, string t) {

vector<vector<int>> char_indexs(26);

for (int i = 0; i < t.size(); i++) {

char_indexs[t[i] - 'a'].push_back(i);

}

int prev_index = -1;

for (auto c : s) {

auto& vec = char_indexs[c - 'a'];

auto ite = std::upper_bound(vec.begin(), vec.end(), prev_index);

if (ite == vec.end()) {

return false;

}

prev_index = *ite;

}

return true;

}

};

415 字符串相加

Question

给定两个字符串形式的非负整数 num1 和num2 ，计算它们的和并同样以字符串形式返回
你不能使用任何內建的用于处理大整数的库（比如 BigInteger），也不能直接将输入的字符串转换为整数形式

Case

示例1

1 2	输入：num1 = "11", num2 = "123" 输出："134"

示例2

1 2	输入：num1 = "456", num2 = "77" 输出："533"

示例3

1 2	输入：num1 = "0", num2 = "0" 输出："0"

Ans1

class Solution {

public:

string addStrings(string num1, string num2) {

int i = num1.size() - 1;

int j = num2.size() - 1;

int carry = 0;

string res;

while (i >= 0 || j >= 0 || carry) {

int sum = carry;

if (i >= 0) {

sum += num1[i--] - '0';

}

if (j >= 0) {

sum += num2[j--] - '0';

}

res += (sum % 10) + '0';

carry = sum / 10;

}

std::reverse(res.begin(), res.end());

return res;

}

};

Ans2

针对上面的处理，当一个字符串长于另一个字符串时，去掉无进位的循环
1. 比如1,1234599，当进位到第三位时，1234不需要再处理了，但上面的算法还是继续循环下去

class Solution {

public:

string addStrings(string num1, string num2) {

int i = num1.size() - 1;

int j = num2.size() - 1;

int carry = 0;

string res;

while (i >= 0 || j >= 0 || carry) {

int sum = carry;

if (i >= 0) {

sum += num1[i--] - '0';

}

if (j >= 0) {

sum += num2[j--] - '0';

}

res += (sum % 10) + '0';

carry = sum / 10;

if (!carry && (i < 0 || j < 0)) {

if (i < 0 && j > 0) {

std::reverse(res.begin(), res.end());

auto temp = num2.substr(0, j + 1);

return temp + res;

} else if (j < 0 && i > 0) {

std::reverse(res.begin(), res.end());

auto temp = num1.substr(0, i + 1);

return temp + res;

}

std::reverse(res.begin(), res.end());

return res;

}

};

Ans3

进阶，如果输入的字符串前面有负号，怎么处理

class Solution {

public:

string add(string num1, string num2) {

int i = num1.size() - 1;

int j = num2.size() - 1;

int carry = 0;

string res;

while (i >= 0 || j >= 0 || carry) {

int sum = carry;

if (i >= 0) {

sum += num1[i--] - '0';

}

if (j >= 0) {

sum += num2[j--] - '0';

}

res += sum % 10 + '0';

carry = sum / 10;

}

std::reverse(res.begin(), res.end());

return res;

}

string sub(string num1, string num2) {

int i = num1.size() - 1;

int j = num2.size() - 1;

int carry = 0;

string res;

while (i >= 0 || j >= 0 || carry) {

int sum = carry;

if (i >= 0) {

sum += num1[i--] - '0';

}

if (j >= 0) {

sum -= num2[j--] - '0';

}

res += (sum + 10) % 10 + '0';

carry = (sum - 10) / 10;

}

std::reverse(res.begin(), res.end());

return res;

}

string addStrings(string num1, string num2) {

bool fn1 = num1[0] == '-';

bool fn2 = num2[0] == '-';

if (fn1) {

num1 = num1.substr(1);

}

if (fn2) {

num2 = num2.substr(1);

}

string final_sign = "";

if (fn1 && fn2) {

final_sign = "-";

} else if (fn1 || fn2) {

if (num1 == num2) {

return "0";

} else if (num1 < num2) {

std::swap(num1, num2);

final_sign = fn1 ? "" : "-";

} else {

final_sign = fn1 ? "-" : "";

}

string res = (fn1 == fn2) ? add(num1, num2) : sub(num1, num2);

return final_sign + res;

}

};

434 字符串中的单词数

Question

统计字符串中的单词个数，这里的单词指的是连续的不是空格的字符
请注意，你可以假定字符串里不包括任何不可打印的字符

Case

示例1

输入: "Hello, my name is John"

输出: 5

解释: 这里的单词是指连续的不是空格的字符，所以 "Hello," 算作 1 个单词

Ans1

class Solution {

public:

int countSegments(string s) {

int count = 0;

bool start = false;

for (auto c : s) {

if (!start && !std::isblank(c)) {

start = true;

}

if (start && std::isblank(c)) {

count++;

start = false;

}

if (start) {

count++;

}

return count;

}

};

Ans2

class Solution {

public:

int countSegments(string s) {

if (s.size() == 0) {

return 0;

}

int count = 0;

int l = 0;

int r = s.size() - 1;

bool fl = true, fr = true;

while (l <= r && (fl || fr)) {

if (std::isblank(s[l])) {

l++;

} else {

fl = false;

}

if (std::isblank(s[r])) {

r--;

} else {

fr = false;

}

if (l > r) {

return 0;

}

for (int i = l+1; i <= r; i++) {

if (std::isblank(s[i]) && !std::isblank(s[i-1])) {

count++;

}

return ++count;

}

};

Ans3

ans1优化

class Solution {

public:

int countSegments(string s) {

int count = 0;

for (int i = 0; i < s.size(); i++) {

// 如果当前字符不是空格且是第一个字符，或它的前一个字符是空格，说明开始了一个新单词

if (!std::isblank(s[i]) && (i == 0 || std::isblank(s[i - 1]))) {

count++;

}

return count;

}

};

459 重复的子串

Question

Case

Ans1

class Solution {

public:

bool repeatedSubstringPattern(string s) {

if (s.size() <= 1) {

return false;

}

string goal;

goal = s[0];

int index = 1;

while (index < s.size()) {

auto temp = s.substr(index, goal.size());

if (temp.size() < goal.size()) {

return false;

}

if (temp == goal) {

index = index + goal.size();

if (index == s.size()) {

return true;

}

} else {

auto sz = goal.size() + 1;

if (sz < s.size()) {

goal = s.substr(0, sz);

index = sz;

} else {

return false;

}

return true;

}

};

Ans2

class Solution {

public:

bool repeatedSubstringPattern(string s) {

if (s.size() <= 1) {

return false;

}

bool flag = true;

char c = s[0];

for (auto i = 1; i < s.size(); i++) {

if (c != s[i]) {

flag = false;

break;

}

if (flag) {

return true;

}

string item;

item = c;

for (int i = 1; i < s.size() / 2; i++) {

item += s[i];

if (s.size() % (i + 1) != 0) {

continue;

}

int index = i + 1;

int len = item.size();

bool flag = true;

while (index < s.size()) {

string temp = s.substr(index, len);

index += len;

if (temp.compare(item) != 0) {

flag = false;

break;

}

if (flag) {

return true;

}

return false;

}

};

Ans3

优化
1. 如果一个字符串不是由子串组成的，那么把它拼接后，它就变成了由子串组成的了
2. 此时，去掉首尾字符后，在剩余部分中必然找不到元串
3. 同理，如果该字符串是由子串组成的，拼接后，取消首尾字符，必然能找到原串

class Solution {

public:

bool repeatedSubstringPattern(string s) {

string ds = s + s;

return (ds.substr(1, ds.size()-2).find(s) != std::string::npos);

}

};

118 杨辉三角
Question
Pic
Case
Tips
Ans1
Ans2
9 回文数
Question
Case
Tips
Ans1
Ans2
13 罗马数字
Question
Case
Tips
Ans
14 最长公共前缀
Question
Case
Tips
Ans
58 最后一个单词的长度
Question
Case
Ans1
Ans2
66 加一
Question
Case
Ans1
Ans2
67 二进制求和
Question
Case
Tips
Ans
125 验证回文串
Question
Case
Tips
Ans1
Ans2
242 有效的字母异位词
Question
Case
Ans1
Ans2
383 赎金信
Question
Case
Ans
387 字符串中的第一个唯一字符
Question
Case
Tips
Ans1
Ans2
389 找不同
Question
Case
Tips
Ans1
Ans2
392 判断子序列
Question
Case
Ans1
Ans2
415 字符串相加
Question
Case
Ans1
Ans2
Ans3
434 字符串中的单词数
Question
Case
Ans1
Ans2
Ans3
459 重复的子串
Question
Case
Ans1
Ans2
Ans3

本文为原创文章，版权归Aet所有，欢迎分享本文，转载请保留出处！

Bingliaolong 关注：0 粉丝：0 最后编辑于：2024-08-16

Everything will be better.