【湘教版数学必修第二册】

平面向量

有向线段

1. 具有方向的线段

位移

$$
\begin{split}
& 就是A到B的直线距离，记作|AB|，\\
& 也就是有向线段 \overrightarrow{AB} 的长度 \\
& 也记作，|\overrightarrow{AB}|
\end{split}
$$

向量

1. 像位移这样既有大小又有方向的量，在数学中称为向量

向量的大小

$$
向量a的大小，也就是向量a的长度，称为a的模，记作 |a|
$$

向量的相等

1. 两次位移，虽然起点不同，但是方向相同，长度相等，就称它们是相等位移
2. 同样，把方向相同，长度相等的向量称为相等向量

相反向量

1. 长度相等，方向相反的向量

$$
\begin{split}
& 如果a，b是相反向量 \\
& 记作，a = -b
\end{split}
$$

零向量

$$
\begin{split}
& 如果a的大小 |a| = 0，则称a是零向量，记作0
\end{split}
$$

1. 约定，所有零向量相等
2. 非零向量的向量，方向是唯一的
3. 零向量的方向是任意的

向量的加法

1. 求向量和的运算

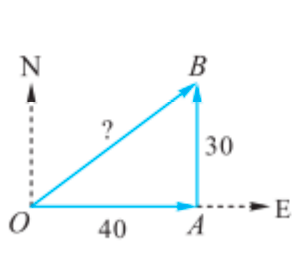
2. 向量加法的三角形法则
   1. 将两个向量表示为首尾相接的有向线段来求和的作图法则

$$
\overrightarrow{OA} + \overrightarrow{AB} = \overrightarrow{OB}
$$

3. 平行四边形法则

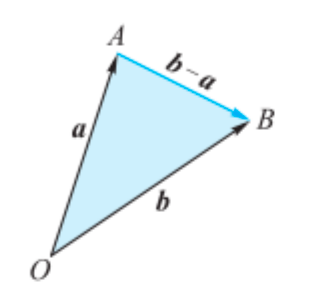
向量的减法

1. 减去一个向量，等于加上它的相反向量

向量的数乘

1. 求向量的实数倍的运算
2. 其几何意义就是把向量沿着它的方向或反方向放大或缩小

共线向量

1. 向量可以用同一条直线上的有向线段或相互平行的有向线段表示
2. 非零向量a，b方向相同或相反，既称a，b共线，也称a，b平行
   1. 用"//"表示
3. 零向量的方向上任意的，所以它与任何一个向量方向相同，因此，零向量与所有的向量平行

$$
a \parallel b
$$

向量夹角

单位向量

1. 把长度为1的向量称为单位向量
2. 对于任意非零向量a，可以得到与它方向相同的唯一单位向量

$$
e = \frac{1}{|a|} a
$$

向量相关运算律

1. 对实数加法的分配律

$$
(x + y) \mathbf{a} = x \mathbf{a} + y \mathbf{a}
$$

2. 对实数乘法的结合律

$$
x (y \mathbf{a}) = (xy) \mathbf{a}
$$

3. 对向量加法的分配律

$$
x (\mathbf{a} + \mathbf{b}) = x \mathbf{a} + x \mathbf{b}
$$

平面向量基本定理

$$
\begin{split}
& 设e_1，e_2是平面上两个不共线向量，则 \\
& 平面上每个向量v都可以分解为e_1,e_2的实数倍之和，即 \\
& v = x e_1 + y e_2, \\
& 其中x, y是实数 \\
& 实数x，y由上面的公式唯一决定，也就是： \\
& 如果v = x e_1 + y e_2 = x' e_1 + y' e_2,则 \\
& x = x', y = y' \\
& 称不共线向量e_1,e_2组成平面上的一组基{e_1, e_2} \\
& 而(x,y)，称为v在这组基下的坐标
\end{split}
$$

平面向量的正交分解

1. 把一个向量分解为两个互相垂直的向量

2. 如上图，平面上互相垂直的单位向量组成的基称为标准正交基

$$
记作{i,j} \\ i = (1,0) \\ j = (0,1)
$$

三角恒等变换

复数

立体几何

概率

数学建模