【湘教版数学必修第一册】

集合概念

集合，集

1. 在数学语言中，把一些对象放在一起考虑时，就说这些对象组成了一个集合或集

集合名称

1. 给这些对象的总的名称，就是这个集合的名字

元素

1. 这些对象中的每一个，都叫作这个集合的一个元素

集合关系

1. 属于
2. 不属于

$$
\begin{split}
& \in \\
& \notin
\end{split}
$$

集合属性

1. 同一集合中的元素是互不相同的
2. 集合中的元素是确定的
   1. 就是给定一个集合，任何一个元素属于或不属于这个集合是确定的
3. 集合中的元素没有顺序

常见集合

1. 自然数集
   1. 全体自然数组成的集合，记作N
   2. N+,N-
2. 整数集
   1. 全体整数组成的集合，记作Z
   2. Z+,Z-
3. 有理数集
   1. 全体有理数组成的集合，记作Q
   2. Q+,Q-
4. 实数集
   1. 全体实数组成的集合，记作R
   2. R+,R-
5. 有限集
   1. 元素个数有限的集合
   2. 或叫有穷集
6. 无限集
   1. 元素无限多的集合
   2. 或叫无穷集
7. 空集
   1. 没有元素的集合
   2. 空气也是有限集

$$
\emptyset
$$

集合的表示

列举法

1. 把集合中的元素一一列举出来

描述法

1. 把集合中元素共有的，也只有该集合中元素才有的属性描述出来，以确定这个集合
2. 一般用于无限集

区间

1. 数学里最常用的一类集合

$$
\begin{split}
& (a, b) \\
& [a, b] \\
& [a, b)
\end{split}
$$

子集

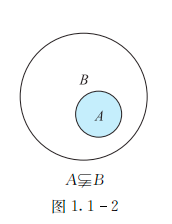
1. 如果集合A的每个元素是集合B的元素，那么A包含于B，或者B包含A

$$
A \subseteq B \\
B \supseteq A
$$

2. 上面的这种关系，称A是B的一个子集
3. 另外，空集包含于任一集合，是任一集合的子集
4. 相等

$$
\begin{split}
& 如果 A \subseteq B ,并且 B \subseteq A \\
& 记作，A = B
\end{split}
$$

5. 真子集

$$
\begin{split}
& 如果 A \subseteq B, 但 A \neq B \\
& 就说A是B的真子集，记作 \\
& A \subsetneq B
\end{split}
$$

6. 韦恩图

全集

1. 如果在某个特定的场合，要讨论的对象都是集合U的元素和子集，就可以约定把集合U叫作全集或基本集

补集

1. 若A是全集U的子集，U中所有不属于A的元素组成的子集叫做A的补集

$$
\begin{split}
& 记作，C_uA \\
& C_uA = {x|x \in U, 且x \notin A }
\end{split}
$$

集合的交并

交集

1. 既属于A又属于B的元素组成的集合

$$
A \cap B = {x|x \in A 且 x \in B}
$$

并集

1. 把集合A和集合B中的元素放在一起组成的集合

$$
A \cup B = {x| x \in A 或 x \in B}
$$

命题相关

命题

1. 命题就是一个陈述句
2. 这个陈述句作出了判断
3. 这种判断可能成立，也可能不成立，两者必居其一且仅局其一，这种语句叫做命题

真命题

1. 成立的命题

假命题

1. 不成立的命题

$$
如果P是一个命题，则"P不成立"也是一个命题，叫做p的否定，记作\neg P
$$

猜想

1. 数学中暂时不知道真假的命题

条件结论

1. 命题通常由条件和结论组成

$$
\begin{split}
& 若P，则Q \\
& P叫做命题的条件 \\
& Q叫做命题的结论
\end{split}
$$

逆命题

1. 条件和结论互换了位置，称一个是另一个的逆命题

充分和必要条件

$$
\begin{split}
& 当“若P，则Q”成立，即 P \rightarrow Q \\
& P叫做Q的充分条件 \\
& Q叫做P的必要条件
\end{split}
$$

1. 就是若P成立，则Q一定也成立。则P对于Q的成立是充分的
2. 若Q不成立，则P必不成立，则Q对P的成立是必要的
3. 如果P成立能推导出Q成立，并且Q成立能推导出P成立，那么P是Q的充分必要条件
   1. 简称充要条件
   2. 如果一个命题和它的逆命题都成立，则此命题都条件和结论互为充要条件

量词相关

$$
对每一个实数x，有x>0 \\
有一个实数x，使x>0
$$

1. 上面的“每一个”，“有一个”，就是量词
2. “每一个”是全称量词
3. “有一个”是存在量词
4. 包含了“任意”，“所有”，“每一个”等全称量词的命题，是全称量词命题

$$
\forall x \in M, p(x)
$$

5. 包含了“存在某个”，“至少有一个”等存在量词的命题，是存在量词命题

$$
\exists x \in M, p(x)
$$

德摩根定律

$$
\neg (p \land q) \rightarrow \neg p \lor \neg q
$$

$$
\begin{split}
& \overline{A \cap B} = \overline{A} \cup \overline{B} \\
& \overline{A \cup B} = \overline{A} \cap \overline{B}
\end{split}
$$

等式不等式相关

性质1

$$
如果a > b,那么b < a \\
如果b < a,那么a > b
$$

性质2

$$
如果a > b, b > c，那么,a > c
$$

性质3

$$
如果a > b, 那么a + c > b + c
$$

推论1

$$
如果a + b > c，那么a > c - b
$$

推论2

$$
如果，a > b, c > d, 那么 a + c > b + d
$$

性质4

$$
如果a > b, c > 0, 那么 ac > bc \\
如果a > b, c < 0, 那么 ac < bc
$$

推论3

$$
如果a > b > 0, c > d > 0, 那么 ac > bd
$$

推论4

$$
如果a > b > 0, 那么 a^n > b^n, (n \in N,n \geq 2)
$$

推论5

$$
如果a > b > 0, 那么 \sqrt{a} > \sqrt{b}
$$

性质5

$$
如果a > b, 且ab > 0，那么 \frac{1}{a} < \frac{1}{b} \\
如果a > b, 且ab < 0，那么 \frac{1}{a} > \frac{1}{b}
$$

基本不等式

1. 算术平均数

$$
\frac{a+b}{2}
$$

2. 几何平均数

$$
\sqrt{ab}
$$

3. 基本不等式

$$
\frac{a+b}{2} \geq \sqrt{ab} \quad (a > 0, b > 0)
$$

4. 应用

$$
如果xy是定值p,那么当且仅当x=y时，和x+y有最小值2\sqrt{p} \\
如果和x+y是定值s，那么当且仅当x=y时，积xy有最大值\frac{s^2}{4}
$$

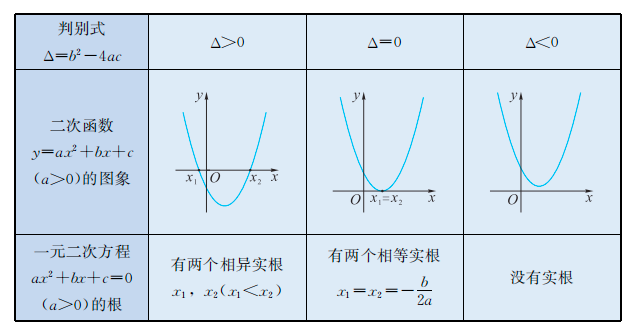
一元二次方程

一元二次不等式

函数相关

函数

$$
\begin{split}
& 设A，B是两个非空的实数集，如果按照某种对应关系f \\
& 对于合集A里面的任何一个数x, 在集合B中都有唯一的数y和它对应 \\
& 那么，称这样的对应关系f为：\\
& f: A \rightarrow B 为定于于A取值于B的函数 \\
& 也记作： \\
& y = f(x) \quad (x \in A , y \in B)
\end{split}
$$

定义域

1. x叫做自变量，x的取值范围A叫做函数的定义域

值域

1. 与x对应的数y叫做函数值，所有函数值组成的集合，叫做函数的值域

相等函数

$$
两个函数f(x)和g(x),当且仅当有相同的定义域U且对每一个x \in U 都有 f(x) = g(x)时，它们相等
$$

函数的表示

1. 解析法

$$
S= x^2 \quad (x \in (0, +\infty))
$$

2. 列表法

3. 图象法

分段函数

函数最值

$$
\begin{split}
& 如果有a \in D, 使得不等式 f(x) \leq f(a)对一切x \in D成立 \\
& 就说f(x)在x = a处取得最大值M=f(x) \\
& M称为f(x)的最大值，a为f(x)的最大值点 \\
& \\
& 最小值同理
\end{split}
$$

单调性

$$
\begin{split}
& 如果对于I上任意两个值x1,x2,当x1<x2时，都有f(x1)<f(x2),就称f(x)是区间I上的增函数 \\
& 也称f(x)在区间I上单调递增 \\
& \\
& 如果对于I上任意两个值x1,x2,当x1 < x2时，都有f(x1)>f(x2),就称f(x)是区间I上的减函数 \\
& 也称f(x)在区间I上单调递减 \\
& \\
& 如果函数y = f(x)在区间I上说增函数或者减函数 \\
& 那么就说函数y=f(x)在这一区间上具有严格的单调性，区间I叫做函数y=f(x)的单调区间
\end{split}
$$

奇偶性

1. 如果函数的图象是以y轴为对称轴的轴对称图形，就称函数是偶函数
2. 如果函数的图象是以原点为中心的中心对称图形，就称函数是奇函数

$$
\begin{split}
& 偶函数 \\
& 如果对一切使F(x)有定义的x，F(-x)也有定义，并且，F(-x)=F(x)成立 \\
& 则F(x)为偶函数 \\
& \\
& 奇函数 \\
& 如果对一切使F(x)有定义的x，F(-x)也有定义，并且，F(-x)=-F(x)成立 \\
& 则F(x)为奇函数
\end{split}
$$

幂函数相关

整数指数幂运算

$$
\begin{split}
& a^m + a^n = a^{m+n} \\
& (a^m)^n = a^{nm} \\
& (ab)^n = a^n b^n
\end{split}
$$

根式

$$
\begin{split}
& 若一个实数x的n次方（n \in N, n \geq 2）等于a \\
& 即 x^n = a \\
& 则称x是a的n次方根
& \\
& \sqrt[n]{a}叫做根式， \quad (n \in N, n \geq 2) \\
& 其中，n叫做根指数，a叫做被开方数
\end{split}
$$

分数指数幂运算

$$
\begin{split}
& 当a大于0，m，n \in N \quad 且 n \geq 2时，规定： \\
& \sqrt[n]{a^m} = a^{\frac{m}{n}} \\
& \frac{1}{\sqrt[n]{a^m}} = a^{-\frac{m}{n}}
\end{split}
$$

有理数指数幂的基本不等式

$$
\begin{split}
& 对任意的正数a>1和有理数r>s，有\frac{a^r}{a^s} = a^{r-s}> 1,即a^r > a^s \\
& 对任意的正数a<1和有理数r>s，有\frac{a^r}{a^s} = a^{r-s}< 1,即a^r < a^s
\end{split}
$$

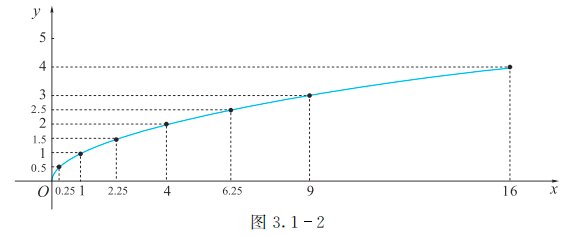
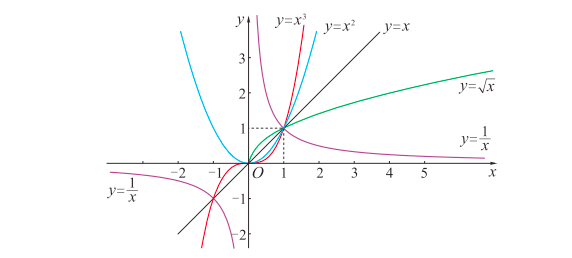
幂函数

$$
\begin{split}
& 对于y = x^a (a \neq 0) \\
& 当a>0时，它在[0,+\infty)有定义且递增，值域为[0,+\infty)，函数图象过(0,0),(1,1)两个点 \\
& 当a<0时，它在(0,+\infty]有定义且递增，值域为(0,+\infty)，函数图象过(1,1)点 \\
& 向上与y轴正向无限接近，向右与x轴正向无限接近
\end{split}
$$

指数函数相关

概念

$$
y = a^x \quad (x \in R) \quad (a > 0, 且 a \neq 1)
$$

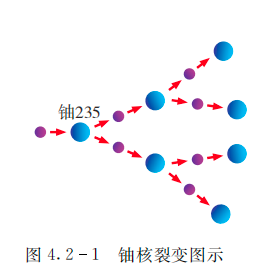
1. 指数爆炸
   1. 当a大于1时，指数函数值随自变量的增长而增大，底数a较大时，指数函数增长速度很快，这是指数爆炸

2. 指数增长

$$
\begin{split}
& 如果把自变量看成时间，在长为T的时间周期[u, u+T]中 \\
& 指数函数y=a^x(a > 1)的值从a^u增长到a^{u+T} \\
& 增长率为(a^{u+T}-a^u) \div a^u = a^T - 1 \\
& 这个值是一个常量 \\
& 在经济学或其他学科中，当某个量在一个既定的时间周期中，其增长百分比是一个常量时 \\
& 这个就被描述为指数式增长，也称指数增长
\end{split}
$$

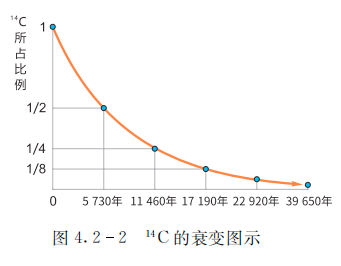
3. 指数衰减

$$
\begin{split}
& 和上面的指数增长反过来 \\
& 如果底数是0<a<1，指数函数值随自变量的增长而缩小以至无限接近于0 \\
& 这种是指数衰减 \\
& 同样得，指数衰减的特点是：在一个既定的时间周期中，其缩小百分比是一个常量
\end{split}
$$

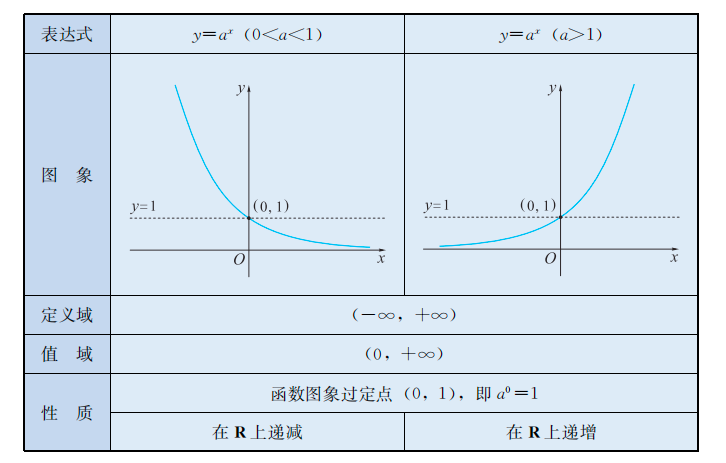
函数特点

$$
\begin{split}
& 经过(0, 1)点 \\
& 并且：\\
& 当a > 1时，指数函数y = a^x 在(-\infty, +\infty)上单调递增 \\
& 当0 < a < 1时，指数函数y = a^x在(-\infty, +\infty)上单调递减
\end{split}
$$

值域

$$
(0, +\infty)
$$

图象

对数函数相关

概念

$$
\begin{split}
& 如果a^b=N \quad (a > 0且 a \neq 1) \\
& 那么：\\
& b叫做以a为底，N的对数 \\
& 记作：\\
& b = log_{a}{N} \\
& 此时：\\
& a叫做对数的底数，N叫做对数的真数
\end{split}
$$

对数的基本恒等式

$$
\begin{split}
& a^{log_a{N}} = N \quad (N > 0, a > 0且a \neq 1) \\
& b = log_a{a^b}
\end{split}
$$

1. 底的对数为1，1的对数为0

对数的运算规则

$$
\begin{split}
& log_a{(M \cdot N)} = log_a{M} + log_a{N} \\
& log_a{M^n} = nlog_a{M} \quad (n \in R) \\
& log_a{\frac{M}{N}} = log_a{M} - log_a{N} \\
& 其中：a > 0且a \neq 1, M > 0, N > 0
\end{split}
$$

对数的换底公式

1. 推导

$$
log_a{N} = log_a{(b^{log_b{N}})} \\
log_a{N} = log_b{N} \cdot log_a{b}
$$

2. 公式

$$
log_b{N} = \frac{log_a{N}}{log_a{b}}
$$

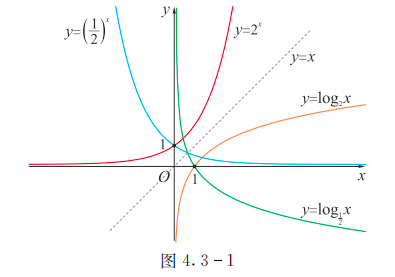
图象

函数与方程

根与零点

$$
\begin{split}
& 一元二次方程ax^2+bx+c =0 的根 \\
& 就是二次函数y = ax^2 + bx + c的零点 \\
& 也就是该函数图象与x轴交点的横坐标
\end{split}
$$

三角函数相关

角的概念

1. 正角
   1. 一条射线绕着端点以逆时针方向选转所成的角
2. 负角
   1. 以顺时针的方向旋转所成的角
3. 零角
   1. 不旋转所成的角
   2. 零角的终边和始边重合

弧度

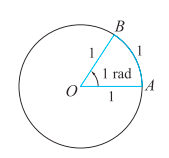
1. 规定把长度等于半径长的弧所对的圆心角叫做1弧度的角

$$
如下图，原半径为1，弧\overset{\frown}{AB} 长等于1，则\angle AOB就是一弧度的角
$$

2. 上面这种以弧度为单位来衡量角的单位制叫做弧度制

角度弧度转换

$$
1^\circ = \frac{\pi}{180}
$$

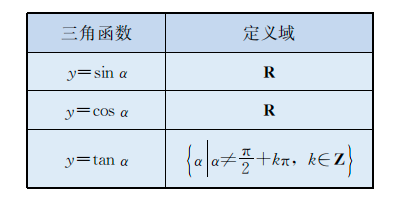
任意角的三角函数

1. 任意角

2. 三角函数

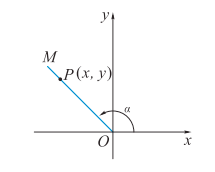
$$
\begin{split}
& sin \alpha = \frac{y}{r} \\
& cos \alpha = \frac{x}{r} \\
& tan \alpha = \frac{y}{x} \\
& 其中， r = \sqrt{x^2+y^2}
\end{split}
$$

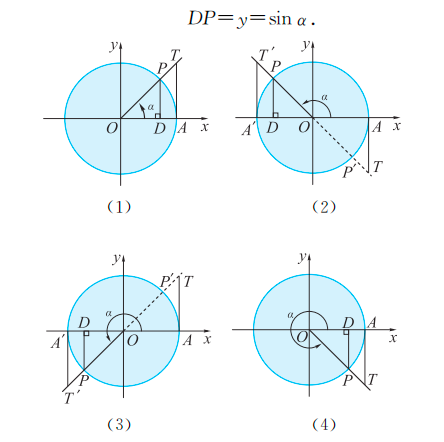
3. 用有向线段表示三角函数

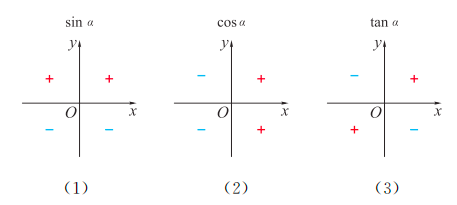
4. 各象限三角函数值的符号
   1. 顺口溜：全是天才
   2. 全：第一象限全(正弦、余弦、正切)是正的
   3. 是：第二象限只有sin是正的
   4. 天：第三象限只有tan是正的
   5. 才：第四象限只有cos是正的

同角三角函数关系

$$
\begin{split}
& sin^{2} \alpha + cos^{2} \alpha = 1 \\
& tan \alpha = \frac{sin \alpha}{cos \alpha}
\end{split}
$$

诱导公式一

$$
\begin{split}
& sin (\alpha +2k\pi) = sin \alpha \\
& cos (\alpha +2k\pi) = cos \alpha \\
& tan (\alpha + 2k\pi) = tan \alpha \\
& 其中， k \in Z
\end{split}
$$

诱导公式二

$$
\begin{split}
& sin (-\alpha) = -sin \alpha \\
& cos (-\alpha) = cos \alpha \\
& tan(-\alpha) = -tan \alpha
\end{split}
$$

诱导公式三

$$
\begin{split}
& sin (\pi + \alpha) = -sin \alpha \\
& cos (\pi + \alpha) = -cos \alpha \\
& tan (\pi + \alpha) = tan \alpha
\end{split}
$$

诱导公式四

$$
\begin{split}
& sin (\pi - \alpha) = sin \alpha \\
& cos (\pi - \alpha) = -cos \alpha \\
& tan (\pi - \alpha) = -tan \alpha
\end{split}
$$

诱导公式五

$$
\begin{split}
& sin (\frac{\pi}{2} - \alpha) = cos \alpha \\
& cos (\frac{\pi}{2} - \alpha) = sin \alpha \\
& sin (\frac{\pi}{2} + \alpha) = cos \alpha \\
& cos (\frac{\pi}{2} + \alpha) = -sin \alpha
\end{split}
$$

诱导公式六

$$
\begin{split}
& tan(\frac{pi}{2} - \alpha) = \frac{sin(\frac{\pi}{2} - \alpha)}{cos(\frac{\pi}{2} - \alpha)} = \frac{cos \alpha}{sin \alpha} = \frac{1}{tan \alpha} \\
& tan(\frac{pi}{2} + \alpha) = \frac{sin(\frac{\pi}{2} + \alpha)}{cos(\frac{\pi}{2} + \alpha)} = \frac{cos \alpha}{-sin \alpha} = -\frac{1}{tan \alpha}
\end{split}
$$

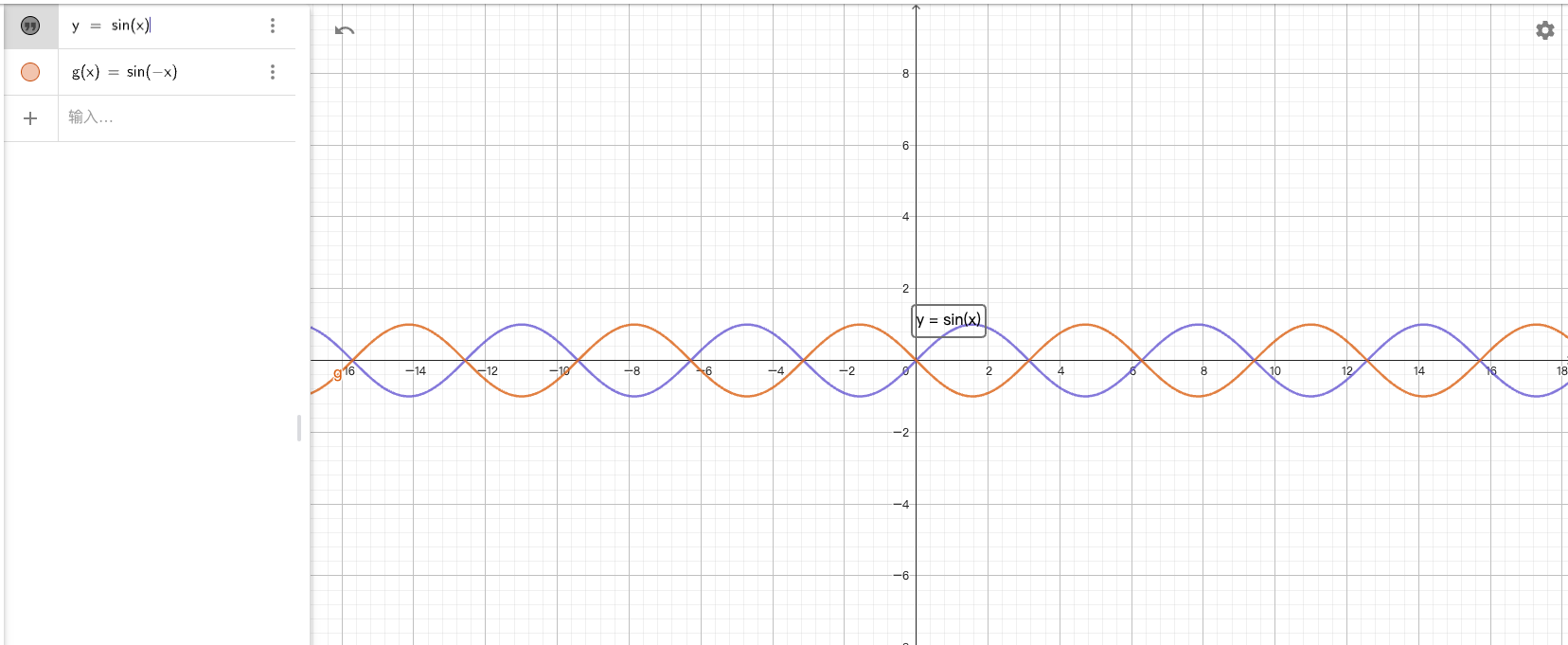
图象

1. 正弦曲线
2. 余弦曲线
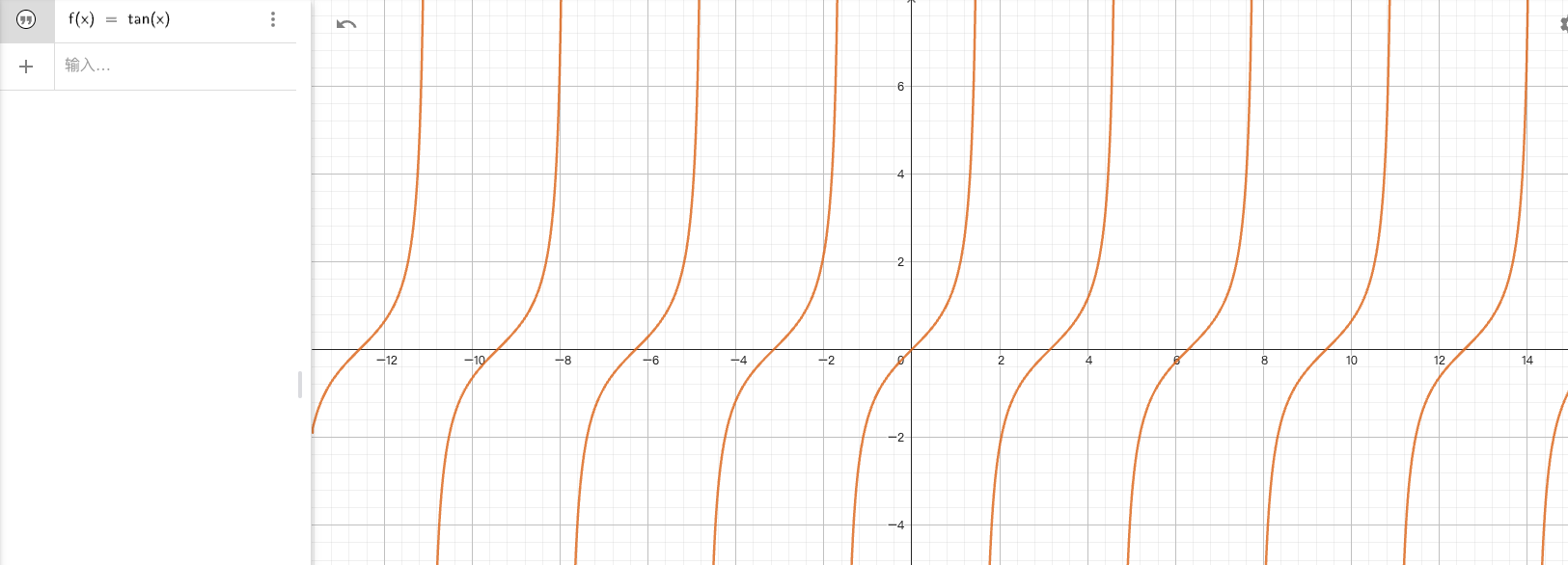
3. 正切曲线

周期性

$$
\begin{split}
& y = A sin(\omega x + \varphi) \\
& 周期 T = \frac{2\pi}{\omega}
\end{split}
$$

奇偶性

统计相关

总体个体

1. 总体
   1. 所要调查的对象的全体
2. 个体
   1. 总体中的成员

样本

1. 从总体中抽取的一部分个体
2. 也叫观测数据

样本容量

1. 构成样本的个体树木
2. 简称样本量

抽样

1. 从总体中抽取样本的工作

统计调查-普查

1. 全面调查
2. 即对需要调查的对象进行逐个调查

统计调查-抽样调查

1. 从调查对象的总体中，抽取若干个个体进行调查

简单随机抽样

$$
\begin{split}
& 一般地，设一个总体含有N个个体，\\
& 从中无放回地抽取n(n \leq N)个个体为样本, \\
& 如果总体内的每个个体都有相同的可能性被抽到，\\
& 这样的抽样方法就是简单随机抽样 \\
& 把抽到的样本叫简单随机样本
\end{split}
$$

1. 常用简单随机抽样方法有：
   1. 抽签法
   2. 随机数法

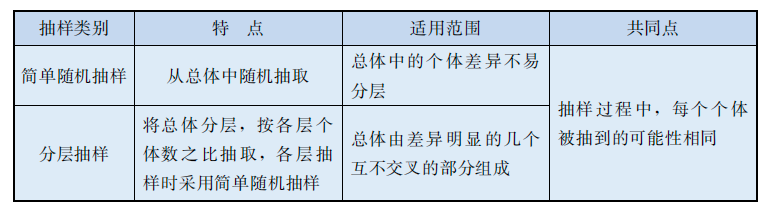
分层抽样

1. 当总体由差异明显的几个部分组成时，为了使抽取的样本更好地反映总体的情况，把总体中各个个体按照某种特征或某种规则划分为互不交叉的层，然后对各层按其在总体中所占比例独立进行简单随机抽样

用样本估计总体

1. 参考数据整理
2. 平均数
3. 众数
   1. 出现次数最多的数
4. 中位数
   1. 位于中间位置的数
5. 极差
   1. 将一组数据中的最大值与最小值统称为极差
   2. 也称全距
6. 方差
   1. 总体方差
   2. 样本方差
7. 标准差
8. 频率