【华东师大版九年级下册】

二次函数

简述

$$
\begin{split}
& 形如 y = ax^2 + bx + c的函数 （开口朝上朝下） \\
& 或，形如x = y^2 +by + c的函数 （开口朝左朝右） \\
& 其中，a,b,c是常数，且 a \neq 0
\end{split}
$$

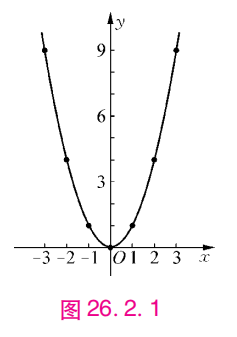
图象

$$
y = x^2
$$

抛物线

1. 像上面的曲线通常叫做抛物线
   1. 它是一个轴对称图形
   2. 与对称轴的交点叫做抛物线的顶点

性质

1. 抛物线有一条对称轴，经过抛物线的顶点
2. 开口方向取决于二次项的系数a
   1. a大于0，抛物线向上或向右
   2. a小于0，抛物线向下或向左
3. 抛物线宽度
   1. a的绝对值越大，抛物线越瘦
   2. a的绝对值越小，抛物线越宽

圆

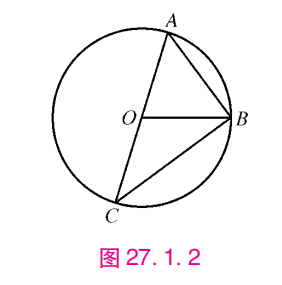
弦

$$
线段AB，BC，AC都是\odot O 中的弦
$$

弧

$$
\begin{split}
& 其中，曲线BC,BAC都是\odot O里面的弧 \\
& 记作， \overset{\frown}{AB} , \overset{\frown}{BAC}
\end{split}
$$

劣弧

1. 小于半圆周的圆弧

优弧

1. 大于半圆周的圆弧

圆心角

$$
\angle AOB , \angle BOC 就是圆心角
$$

性质

1. 同一个圆中，如果圆心角相等，那么它们所对的弧相等，所对的弦相等
2. 同一个圆中，如果弧相等，那么它们对应的圆心角相等，所对的弦相等
3. 同一个圆中，如果弦相等，那么它们所对的圆心角相等，所对的弧相等

轴对称

1. 圆是轴对称图形，它的任意一条直径所在的直线都是它的对称轴

垂径定理

1. 垂直于弦的直径平分这条弦，并且平分这条弦所对的两条弧
2. 平分弦（不是直径）的直径垂直于这条弦，并且平分这条弦所对的两条弧
3. 平分弧的直径垂直平分这条弧所对的弦

圆周角定理

1. 在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于该弧所对的圆心角的一半
2. 相等的圆周角所对的弧相等

圆周角定理推论1

1. 90度的圆周角所对的弦是直径

圆周角定理推论2

1. 圆内接四边形的对角互补

三点定圆

1. 不在同一条直线上的三个点确定一个圆
2. 经过这个三角形顶点的这个圆，就是这个三角形的外接圆
3. 三角形外接圆的圆心叫这个三角形的外心
   1. 三角形的外心就是三角形三条边的垂直平分线的交点
4. 相对地，这个三角形就是这个圆的内接三角形

外心

1. 三角形外接圆的圆心叫这个三角形的外心
2. 三角形的外心就是三角形三条边的垂直平分线的交点

直线与圆的关系

1. 相离
2. 相切
   1. 此时这条直线是这个圆的切线，公共点叫做切点
3. 相交
   1. 此时这条直线是这个圆的割线

圆的切线的判定定理

1. 经过圆的半径的外端切垂直于这条半径的直线是圆的切线

圆的切线的性质定理

1. 圆的切线垂直于经过切点的半径

切线长定理

1. 过圆外一点所画的圆的两条切线，它们的切线长相等。
2. 这一点和圆心的连线平分这两条切线的夹角

内切圆

1. 与三角形各边都相切的圆，叫这个三角形的内切圆

内心

1. 三角形的内切圆的圆心叫做这个三角形的内心
2. 三角形的内心就是三角形三条角平分线的交点

圆的面积

$$
S = \pi r^2
$$

圆的周长

$$
\begin{split}
& C = 2 \pi r \\
& 或者 \\
& d = 2r
& C = \pi d
\end{split}
$$

弧长公式

$$
\begin{split}
& l = \frac{n}{360} \cdot 2\pi r \\
& \rightarrow \\
& l = \frac{n \pi r}{180}
\end{split}
$$

扇形面积

$$
\begin{split}
& S = \frac{n}{360} \cdot \pi r^2 \\
& \quad = \frac{1}{2} \cdot \frac{n \pi r}{180} \cdot r \\
& \quad = \frac{1}{2} l r \\
& 或者 \\
& S = \frac{1}{2}lr
\end{split}
$$

正多边形和圆

1. 任何正多边形都有一个外接圆和一个内切圆

样本与总体

总体

1. 把所要考察的对象的全体叫做总体

个体

1. 把组成总体的每一个考察对象叫做个体

样本

1. 从总体中取出的一部分个体叫做这个总体的一个样本

容量

1. 一个样本包含的个体的数量叫做这个样本的容量