【华东师大版九年级上册】

二次根式

概念

$$
形如 \sqrt{a} \qquad (a \geq 0) 的式子，叫二次根式。
$$

乘法

$$
\sqrt{a} \cdot \sqrt{b} = \sqrt{ab} \qquad (a \geq 0, b \geq 0)
$$

积的算术平方根

$$
\sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \qquad (a \geq 0, b \geq 0)
$$

除法

$$
\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}} \qquad(a \geq 0, b > 0)
$$

一元二次方程

直接开平方法

因式分解法

配方法

1. 在方程两边同时加上一个适当的数，让左边配成一个含有未知数的完全平方式，右边是一个常数

公式法

$$
\begin{split}
& ax^2 + bx + c = 0 \qquad (a \ne 0) \\
& x = -\frac{b}{2a} \pm \frac{\sqrt{b^2-4ac}}{2a} \qquad (b^2 - 4ac \geq 0) \\
& x_1 = -\frac{b}{2a} + \frac{\sqrt{b^2-4ac}}{2a} \qquad (b^2 - 4ac \geq 0) \\
& x_2 = -\frac{b}{2a} - \frac{\sqrt{b^2-4ac}}{2a} \qquad (b^2 - 4ac \geq 0)
\end{split}
$$

根的判别式

$$
\begin{split}
& \qquad (b^2 - 4ac > 0)，两个不相等的实数根 \\
& \qquad (b^2 - 4ac = 0)，两个相等的实数根 \\
& \qquad (b^2 - 4ac < 0)，没有实数根
\end{split}
$$

根与系数的关系

1. 二次项系数为1的一元二次方程根与系数的关系

$$
\begin{split}
& 设一元二次方程 x^2 + px + q = 0的两根为x_1，x_2，那么: \\
& x_1 + x_2 = -p \\
& x_1 \cdot x_2 = q
\end{split}
$$

图形

成比例线段

$$
\begin{split}
& 如果，\frac{a}{b} = \frac{c}{d}，那么，ad = bc \\
& 如果，ad = bc，那么，\frac{a}{b} = \frac{c}{d}
\end{split}
$$

平行线分线段成比例

1. 两条直线被一组平行线所截，所得的对应线段成比例

相似图形

1. 相似多边形的对应边成比例，对应角相等

相似三角形

$$
\begin{split}
& \frac{AB}{A'B'} = \frac{BC}{B'C'} = \frac{CA}{C'A'} = k \\
& \angle A = \angle A', \angle B = \angle B', \angle C = \angle C' \\
& \triangle ABC \sim \triangle A'B'C'
\end{split}
$$

1. 平行于三角形一边的直线，和其他两边相交（或两边的延长线）相交所构成的三角形与原三角形相似

相似三角形的判定定理1

1. 两角分别相等的两个三角形相似

相似三角形的判定定理2

1. 两边成比例切夹角相等的两个三角形相似

相似三角形的判定定理3

1. 三边成比例的两个三角形相似

相似三角形的性质

1. 相似三角形对应边上的高的比等于相似比
2. 相似三角形面积的比等于相似比的平方

中位线

1. 把连接三角形两边中点的线段叫做三角形的中位线
2. 三角形的中位线平行于第三边，并且等于第三边的一半

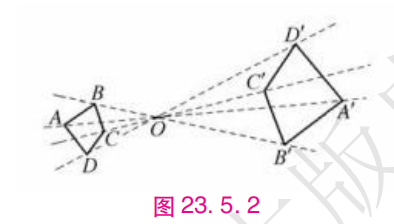
位似图形

$$
\begin{split}
& 两个图形的对应点A和A'、B和B'、C和C'...的连线都相交于一点O， \\
& 并且 \frac{OA'}{OA} = \frac{OB'}{OB} = \frac{OC'}{OC} = k \\
& 这两个图形叫位似图形 \\
& 其中，点O是位似中心
\end{split}
$$

如图：

三角形

直角三角形性质1

1. 直接三角形的两个锐角互余

直角三角形性质2

1. 直接三角形两直角边的平方和等于斜边的平方

直角三角形性质3

1. 直角三角形斜边上的中线等于斜边的一半

三角函数

$$
\begin{split}
& \sin{A} = \frac{\angle A的对边}{斜边} = \frac{a}{c} , （正弦）\\
& \cos{A} = \frac{\angle A的邻边}{斜边} = \frac{b}{c} , （余弦）\\
& \tan{A} = \frac{\angle A的对边}{\angle A的邻边} = \frac{a}{b} , （正切）
\end{split}
$$

事件和概率

必然事件

1. 每次实验中都一定会发生的事件

不可能事件

1. 每次实验中都一定不会发生的事件

确定事件

1. 上面这两种事件在实验中是否发生都是我们能够预先确定的，通常确定事件
   1. 必然事件
   2. 不可能事件

随机事件

1. 无法预先确定在一次实验中会不会发生的事件

概率

1. 一个事件发生的可能性

$$
\begin{split}
& 如，抛硬币，假设每次抛出要么是正面，要么是反面 \\
& 那，“出现反面”这个事件的概率则是\frac{1}{2} \\
& 记为： P = \frac{1}{2}
\end{split}
$$

2. 概率值在0和1之间
   1. 0表示不可能发生
   2. 1表示一定会发生
3. 公式：

$$
P(事件) = \frac{有利于事件的情况数量}{所有可能得情况数量}
$$

频率

1. 在一定数量的试验或观察中，某个特定事件发生的次数
   1. 它是一个实际观测到的数值，基于实际发生的事件
2. 公式：

$$
f(事件) = \frac{事件发生的次数}{所有试验的次数}
$$

概率和频率区别

1. 概率是理论上的预期，而频率是实际发生的情况
2. 概率是基于所有可能性的理论计算，而频率是基于实际发生的事件的统计
3. 概率用于预测事件发生的可能性，而频率用于描述过去发生事件的频繁程度
4. 当试验次数足够多时，特定事件的频率通常会接近其概率值