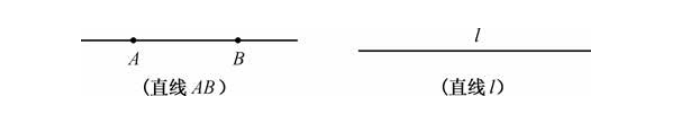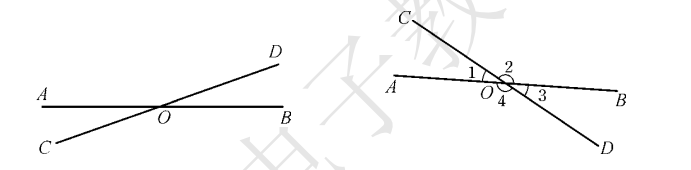有理数
范围
- 整数
- 正整数
- 0
- 负整数
- 分数
- 正分数
- 负分数
概念
- 非负整数或自然数集
- 正整数
- 0
数轴
- 直线
- 原点
- 正方向
- 刻度
相反数
- 只有正负号不同的两个数,互为相反数
- 0的相反数是0
绝对值
- 数轴上表示数a的点与原点的距离叫做数a的绝对值
$$
\vert a \vert
$$
- 正数的绝对值是它本身
- 0的绝对值是0
- 负数的绝对值是它的相反数
$$
\vert a \vert \ge 0
$$
有理数加法
- 同号相加,取加数相同的正负号,并把绝对值相加
- 绝对值不相等的异号两数相加,取绝对值大的数的正负号,并用较大的绝对值减去较小的绝对值
- 互为相反数的两个数,相加得0
- 一个数与0相加,仍得到这个数
有理数加法运算律
交换律
$$
a + b = b + a
$$
结合律
$$
(a + b) + c = a + (b + c)
$$
有理数减法
- 减去一个数,等于加上这个数的相反数
有理数乘法
- 两数相乘,同号得正,异号得负,并把绝对值相乘
- 任何数与0相乘都得0
有理数乘法运算律
交换律
$$
a \cdot b = b \cdot a
$$
结合律
$$
(a \cdot b) \cdot c = a \cdot (b \cdot c)
$$
分配律
$$
a \cdot (b + c) = a \cdot b + a \cdot c
$$
倒数
- 乘积是1的两个数互为倒数
- 除以一个数等于乘以这个数的倒数
- 零不能作除数
有理数除法
- 两数相除,同号得正,异号得负,并把绝对值相除
- 0除以任何一个不为0的数,都得0
有理数乘方
- a是底数
- n是指数
- 乘方的结果叫幂
$$
a^n
$$
- 正数的任何次幂都是正数
- 负数的奇次幂是负数,负数的偶次幂是正数
科学计数法
$$
a \times 10^n \qquad (1 \le a \lt 10)
$$
有理数的混合运算
- 先乘方,再乘除,最后加减
- 同级运算,从左往右
- 有括号,先小括号,再中括号,最后大括号
近似数
四舍五入
精度
- 精确到十分位(0.1)
- 精确到百分位(0.01)
- 精确到千分位(0.001)
整式相关
列代数式
- 用字母来表示数字的各种运算
代数式
- 由数字和字母用运算符号连接成的式子(如下所示)
$$
\begin{split}
&1\\
&2a\\
&100t - 200t\\
&ab\\
&5.6f\\
&\frac{199}{t}
\end{split}
$$
代数式的值
- 根据运算关系,等于结果,就是求代数式的值
单项式
- 由数字和字母的乘积组成的代数式,就是单项式
$$
\begin{split}
&1\\
&2a\\
&ab\\
&5.6f
\end{split}
$$
- 单项式的数字因数,叫单项式的系数
$$
\begin{split}
&1 \qquad \rightarrow \qquad 1\\
&2a \qquad \rightarrow \qquad 2\\
&ab \qquad \rightarrow \qquad 1\\
&5.6f \qquad \rightarrow \qquad 5.6
\end{split}
$$
- 单项式中,所有字母的指数的和,叫这个单项式的次数
$$
\begin{split}
&1 \qquad \rightarrow \qquad 常数项相当于乘了x的0次,所以次数是0\\
&2a \qquad \rightarrow \qquad a的指数是1,所以是1次\\
&ab \qquad \rightarrow \qquad a指数是1,b指数是1,加起来单项式ab次数是2\\
&5.6f \qquad \rightarrow \qquad 5.6 f的指数是1,所以是1次
\end{split}
$$
多项式
- 几个单项式的和
- 多项式里面的每个单项式,叫多项式的项
- 不含字母的项,叫常数项
$$
ab + 1 -2b
$$
整式
- 单项式和多项式,统称整式
降幂排序
- 按多项式里面字母的指数从大到小排序
$$
-2x^3+5x^2+3x-1
$$
升幂排序
- 按多项式里面字母的指数从小到大排序
$$
-1+3x+5x^2-2x^3
$$
同类项
- 包含的字母相同,并且字母的指数相等的,是同类项
$$
\begin{split}
&3x-2y+1+3y-2x-5\\
&同类项:3x \qquad -2x\\
&同类项:-2y \qquad 3y\\
&同类项:1 \qquad -5
\end{split}
$$
合并同类项
- 把同类项的系数相加,所得结果作为系数,字母和字母的指数保持不变
$$
\begin{split}
&3x-2y+1+3y-2x-5\\
&同类项:3x \qquad -2x \qquad 合并后 \rightarrow x\\
&同类项:-2y \qquad 3y \qquad 合并后 \rightarrow y\\
&同类项:1 \qquad -5 \qquad 合并后 \rightarrow -4\\
&最后结果 \rightarrow x + y - 4
\end{split}
$$
提取括号
- 括号前面是+号,把括号前面的+号去掉,并且把括号去掉,括号里面的各项,不变符号
$$
a + (b - c) \qquad \rightarrow \qquad a + b - c
$$
- 括号前面是-号,把括号前面的-号去掉,并且把括号去掉,括号里面的各项,变符号
$$
a - (b + c - d) \qquad \rightarrow \qquad a - b - c + d
$$
整式的加减
- 先去括号,在合并同类项
图形相关
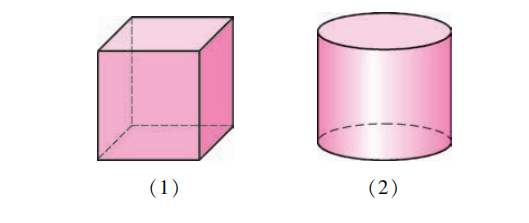
柱体
- 柱体分为:
- 棱柱(有各种棱柱,三棱柱、四棱柱、五棱柱等等)
- 圆柱
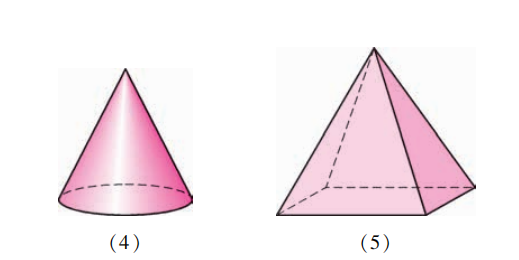
椎体
- 椎体分为:
- 棱锥(有各种棱锥,三棱锥、四棱锥、五棱锥等等)
- 圆锥
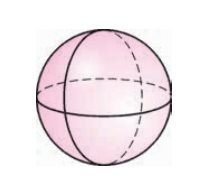
球体
多面体
- 像上面的立体图形,就叫多面体
三视图
- 主视图
- 就是从前往后看,看到的平面图形
- 左视图
- 就是从左往右看,看到的平面图形
- 俯视图
- 就是从上往下看,看到的平面图形
立体图形表面展开图
- 就是把立体图形沿着边剪开,然后能平铺在平面上,看到的图形
点和线段
- 在平面上画一个点,并用一个字母A来表示,就是点A
- 把两个在平面上的点用直线连起来,就是线段
- 两点之间,线段最短
射线
- 把线段向一个方向无限延伸,形成的图形,就是射线
直线
- 把线段向两方无限延伸,形成的图形,就是直线
- 经过两点有一条直线,并且只有一条直线
- 也就是说,两点确定一条直线
线段运算

$$
\begin{split}
&AB + BD = AD\\
&这个等式看图很容易观察出来\\
&既然是等式,也就是说,可以根据运算,换成减法的\\
&AD - BD = AB\\
&这个减法等式看图也很容易观察出来
\end{split}
$$
欧拉公式
$$
定点数 + 面数 - 棱数 = 2
$$
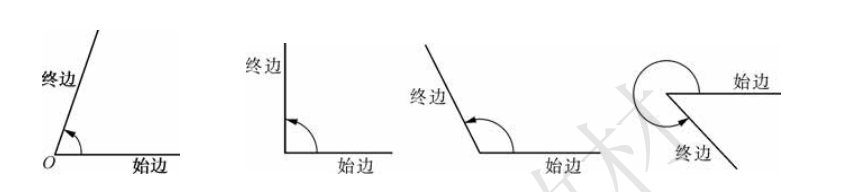
角
- 要观察它的始边,始边到终边,才是这个角的角度
平角
- 始边和终边在同一直线上了
周角
- 始边和终边重合了
角的换算
- 1周角是360度
- 1平角是180度
- 1度是60分
- 1分是60秒
角的比较
角的加减
角的平分线
- 从一个角的顶点引出一条射线,把这个角分成两个相等的角,这条射线,就是这个角的平分线
余角
- 两个角的和等于90度,这两个角互为余角,简称互余
补交
- 两个角的和等于180度,这两个角互为补交,简称互补
平行线相关
对顶角
- 两条线相交,只有一个交点
- 如图,角1和角3是对顶角;角2和角4是对顶角
- 对顶角相等
垂线、垂足
- AB和CD垂直,交点O,叫垂足
- AB是CD的垂线,CD是AB的垂线
- 过一点有且只有一条直线与已知直线垂直
垂线段
- 线段AB与直线l垂直,线段AB叫点A到直线l的垂线段
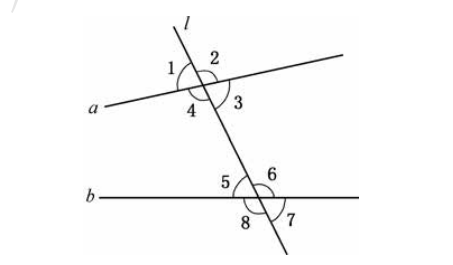
同位角
- 角1和角5处于直线l的同一侧,且分别在直线a、b的同一方,它们就是同位角
内错角
- 角3和角5处于直线l的不同侧,且在直线a、b的不同方,题目就是内错角
同旁内角
- 角4和角5位于直线l的同一侧,且在直线a、b的不同方,它们就是同旁内角
平行线
- 同一平面内不想交的两条直线,叫平行线
- 过直线外一点,有且只有一条直线与这条直线平行
平行线性质
- 两直线平行,同位角相等
- 两直线平行,内错角相等
- 两直线平行,同旁内角互补
判断两直线平行的方法
- 如果同位角相等,两直线平行
- 如果内错角相等,两直线平行
- 如果同旁内角互补,两直线平行
- 同一平面内,垂直于同一条直线的两条直线平行
本文为原创文章,版权归Aet所有,欢迎分享本文,转载请保留出处!
你可能也喜欢
- ♥ 【湘教版数学必修第一册】12/28
- ♥ 【华东师大版九年级下册】12/11
- ♥ 【华东师大版八年级下册】05/16
- ♥ 【华东师大版九年级上册】05/31
- ♥ 【湘教版数学必修第二册】01/31
- ♥ 【华东师大版八年级上册】03/21