大话数据结构_图表示

1-邻接矩阵

1. 图的邻接矩阵存储方式是用两个数组来表示图。
   1. 一个一维数组存储图中的顶点信息。
   2. 一个二维数组（称为邻接矩阵）存储图中的边或弧的信息。
2. 设图G有n个顶点，则邻接矩阵是一个n*n的方阵，定义为：

$$
arc[i][j] =
\begin{cases}
1, \qquad 若(v_i,v_j)\in E 或<v_i,v_j> \in E \\
0, \qquad 反之
\end{cases}
$$

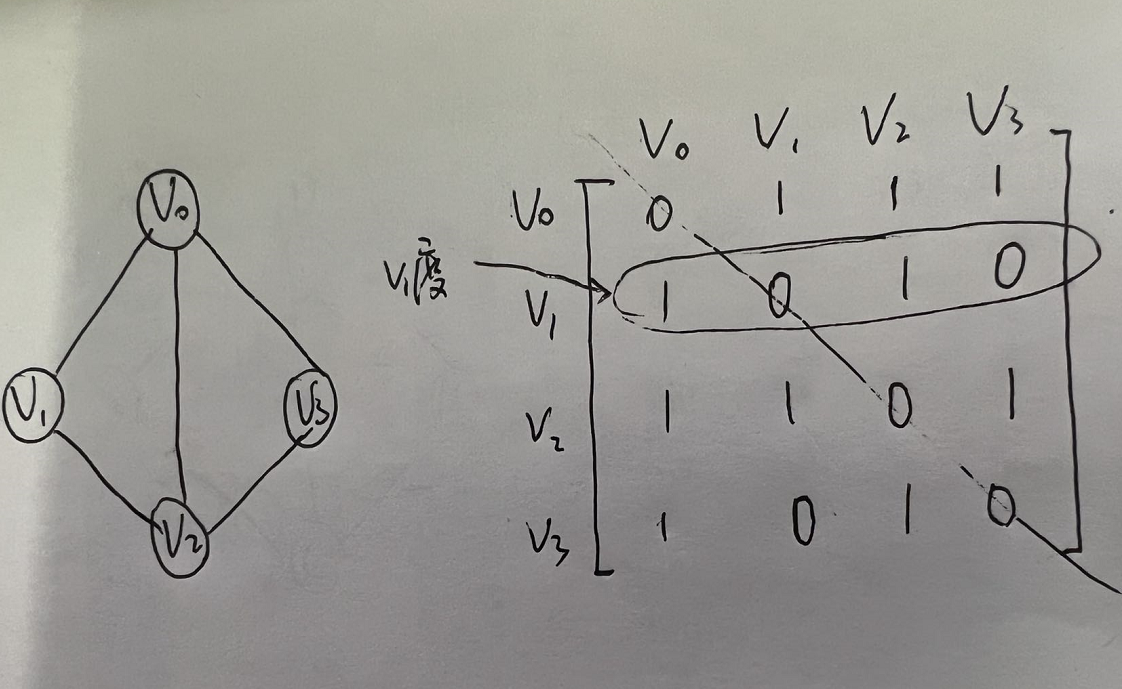
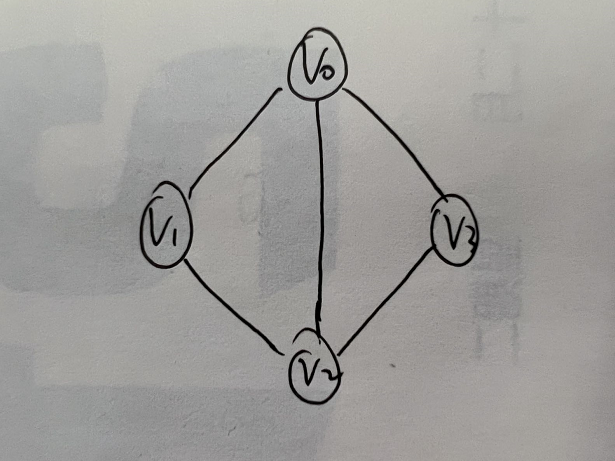
3. 由上述算式，无向图的边数组是一个对称矩阵
   1. 某个顶点的度，就是这个顶点$v_i$在邻接矩阵中第i行（或第i列）的元素之和。
   2. 顶点$v_i$的所有邻接点就是将矩阵中第i行元素扫描一遍，arc[i][j]为1，就是邻接点。

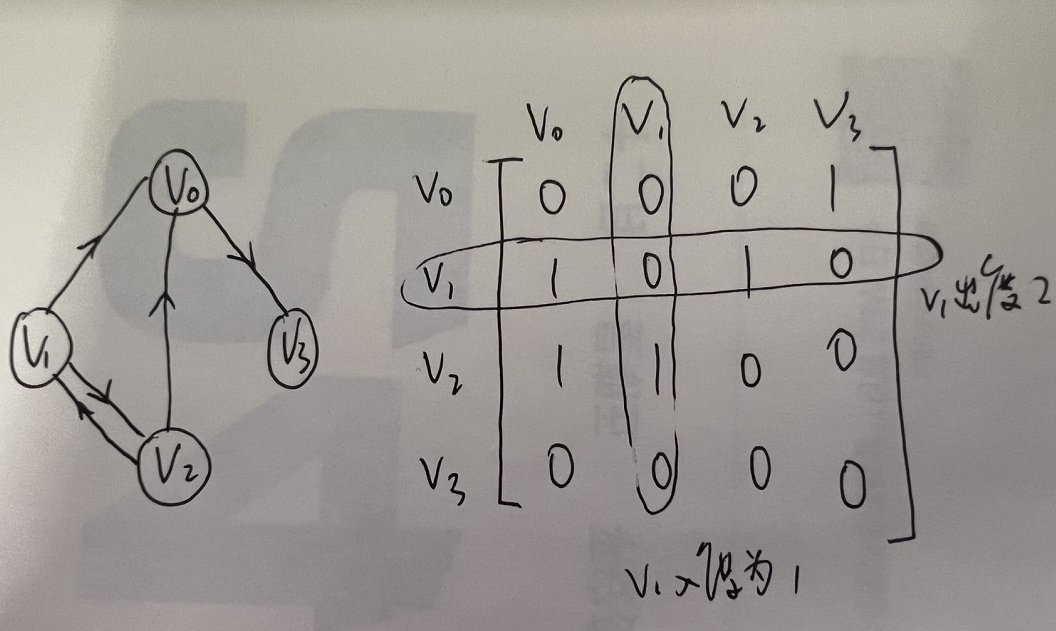
4. 对于有向图：
   1. 判断顶点$v_i$和$v_j$是否存在弧，只需要查找矩阵中arc[i][j]是否为1即可。
   2. $v_i$的所有邻接点就是将矩阵第i行元素扫描一遍，查找arc[i][j]为1的顶点。

网图

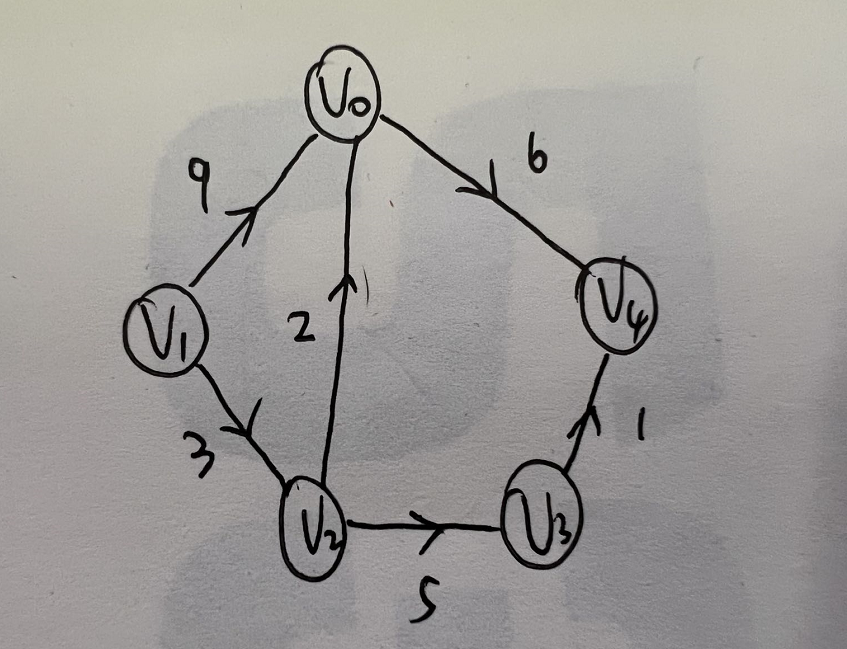
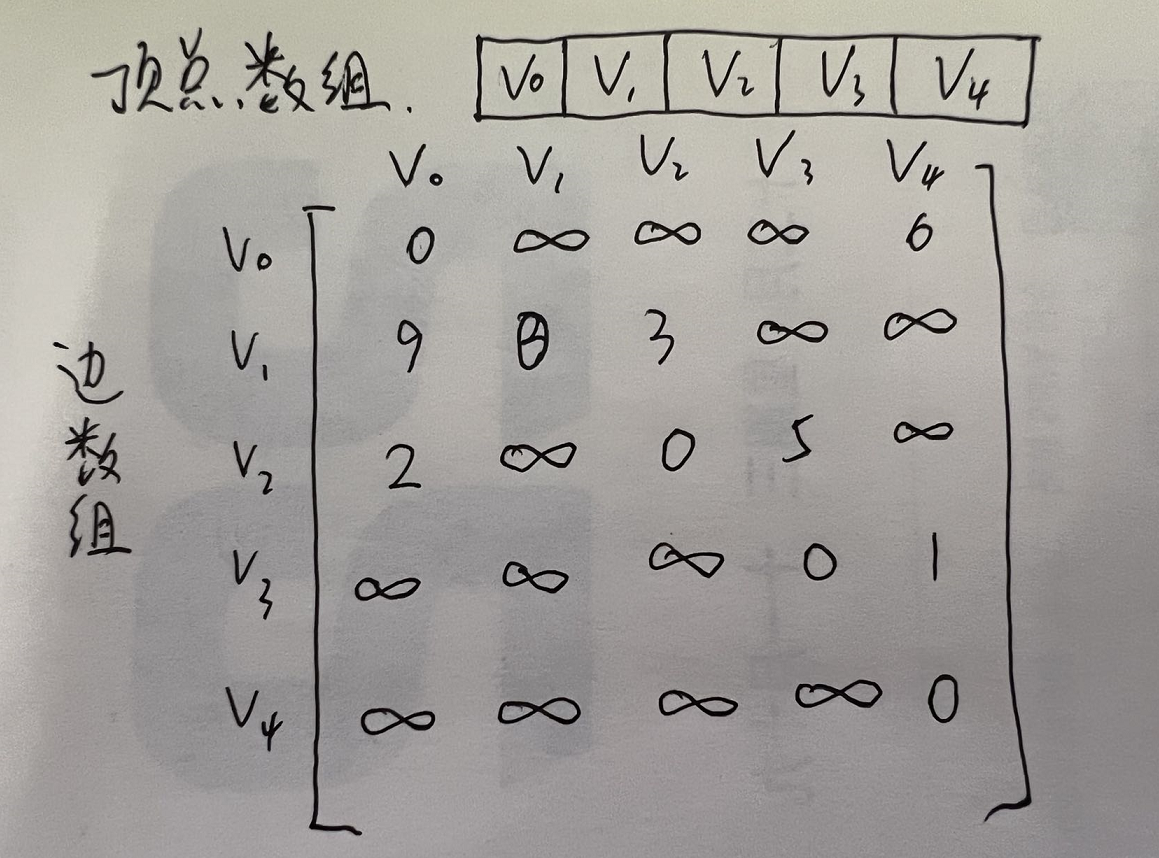
1. 设图G是网图，有n个顶点，则邻接矩阵是一个n*n的方阵，定义如下：

$$
arc[i][j] = \begin{cases}
W_{ij}, \qquad 若(v_i,v_j) \in E 或 <v_i, v_j> \in E \\
0, \qquad 若i = j \\
\infty, \qquad 反之
\end{cases}
$$

2. $w_{ij}$表示$(v_i,v_j)$或$<v_i, v_j>$上的权值。
3. $\infty$表示一个计算机允许的、大于所有边上的权值的值，也就是一个不可能的极限值。

邻接矩阵创建

2-邻接表

1. 邻接矩阵是一种还不错的图存储结构，但是对于边数相对顶点较少的图，这种结构是存在对存储空间的极大浪费的。
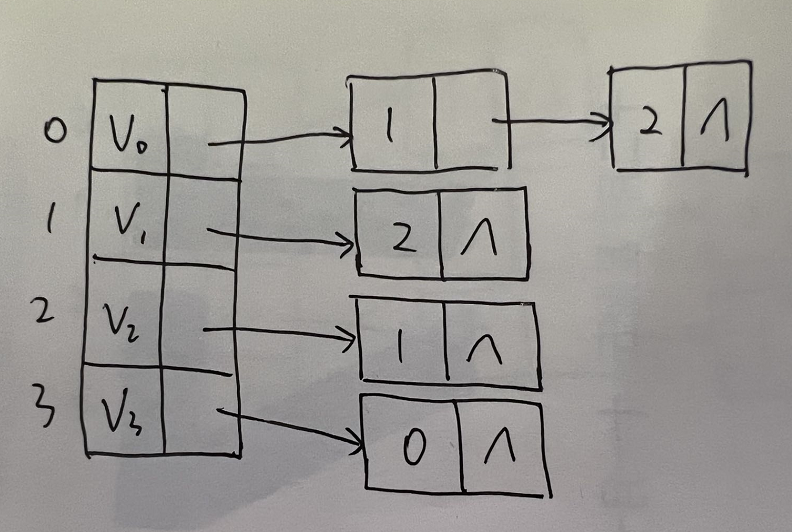
2. 邻接表：
   1. 图中顶点用一个一维数组存储（也可以用单链表存储）。对于顶点数组中，每个数据元素还需要存储一个指向第一个邻接点的指针，以便于查找该顶点的信息。
   2. 图中每个顶点$v_i$的所有邻接点构成一个线性表，由于邻接点的个数不定，所有用单链表存储，无向图称为顶点$v_i$的边表，有向图则称为顶点$v_i$作为弧尾的出边表。

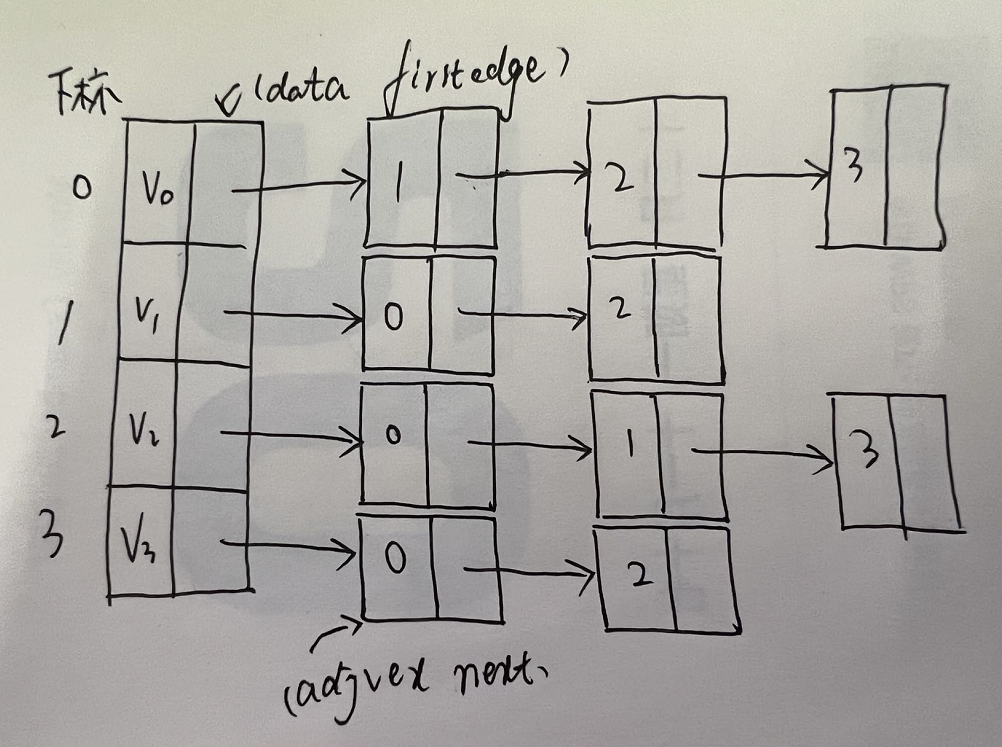
3. 从上图，顶点表的各个结点是由data和firstedge两个域表示，data是数据域，存储顶点的信息，firstedge是指针域，指向边表的第一个结点。即此顶点的第一个邻接点。
   1. 边表是由adjvex和next两个域组成，adjvex是邻接点域，存储某顶点的邻接点在顶点表中的下标，next则存储指向边表中下一个结点的指针。

邻接表：

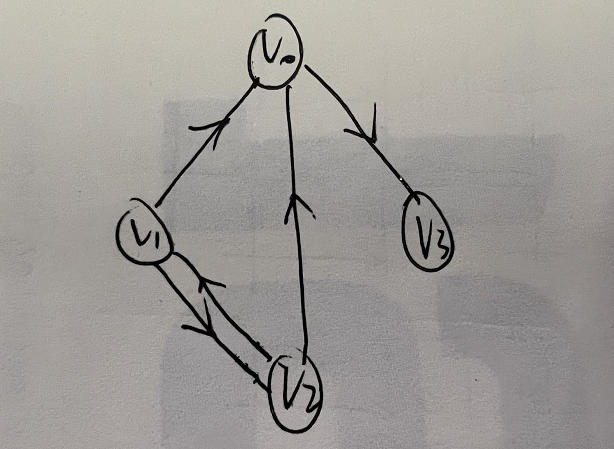
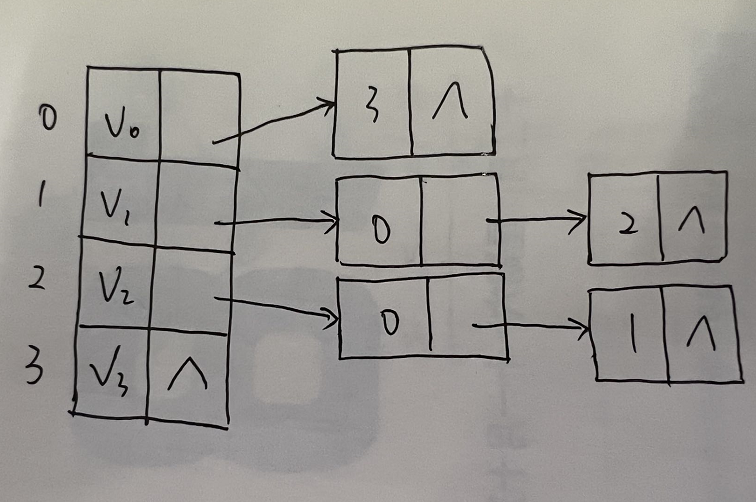
逆邻接表：

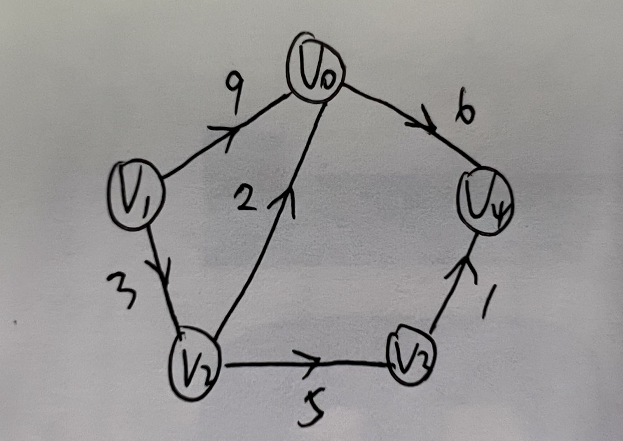
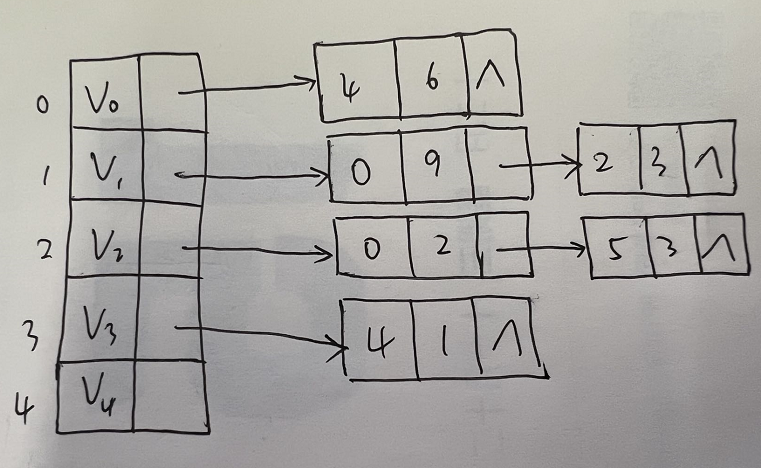
带权网图：

3-十字链表

1. 将邻接表和逆邻接表结合起来，就是十字链表。
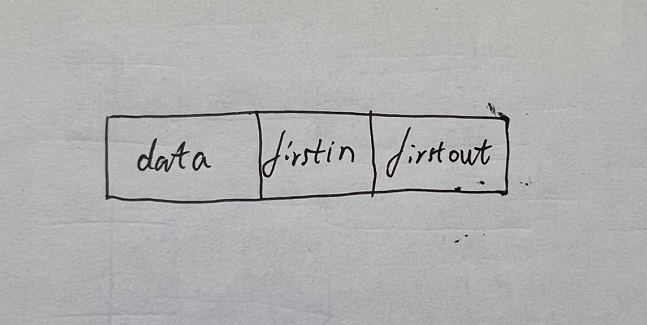
2. 顶点表结点：
   1. firstin表示入边表头指针，指向该顶点的入边表中第一个结点
   2. firstout表示出边表头指针，指向该顶点的出边表中的第一个结点

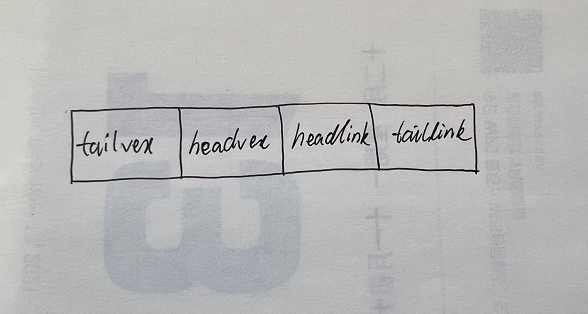
3. 边表结点：
   1. tailvex是指弧起点在顶点表的下标
   2. headvex是指弧终点在顶点表中的下标
   3. headlink是指入边表指针域，指向终点相同的下一条边
   4. taillink是指边表指针域，指向起点相同的下一条边
   5. 如果是网，还可以增加一个weight域来表示权值

4. 十字链表的好处就是把邻接表和逆邻接表整合到一起，这样既容易找到以$v_i$为尾的弧，也容易找到以$v_i$为头的弧，因而容易求得顶点的出度和入度。
   1. 除了结构复杂一点，创建图算法的时间复杂度和邻接表是相同的。
   2. 在有向图的应用中，十字链表是非常好的数据结构模型。

4-邻接多重表

5-边集数组

1. 边集数组是由两个一维数组构成
   1. 一个存储顶点的信息
   2. 一个存储边的信息，这个边数组每个元素由一条边的起点下标、终点下标和权组成