大话数据结构_图

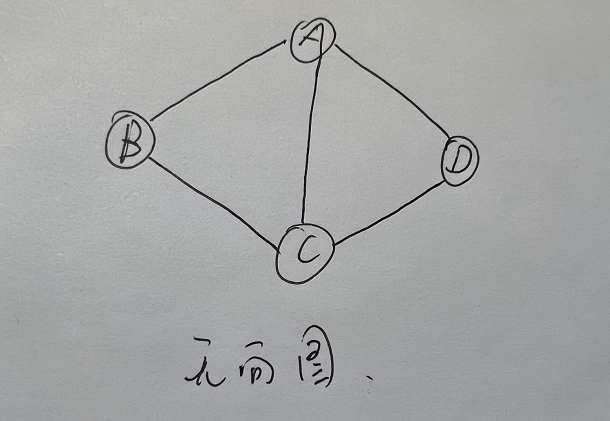
概述

1. 图是一种较线性表和树更加复杂的数据结构。
   1. 在图形结构中，结点之间的关系可以是任意的，图中任何两个数据元素之间都可能相关。
2. 图是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G(V,E)，其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。
   1. 线性表中把数据元素叫元素，树中叫结点，图中称为顶点。
   2. 线性表中没有数据元素，称为空表。树中没有结点，称为空树。在图中，不允许没有顶点。
   3. 线性表中，相邻的数据元素之间具有线性关系。树结构中，相邻两层的结点具有层次关系。而图中，任意两个顶点之间都可能存在关系，顶点之间的逻辑关系用边来表示，边集可以是空的。

无向边

1. 若顶点$v_i$到$v_j$之间的边没有方向，则称这条边为无向边，用无序偶对（$v_i$,$v_j$）来表示。

无向图

1. 如果图中任意两个顶点之间的边都是无向边，该图为无向图。

无向完全图

1. 在无向图中，如果任意两个顶点之间都存在边，则该图为无向完全图。
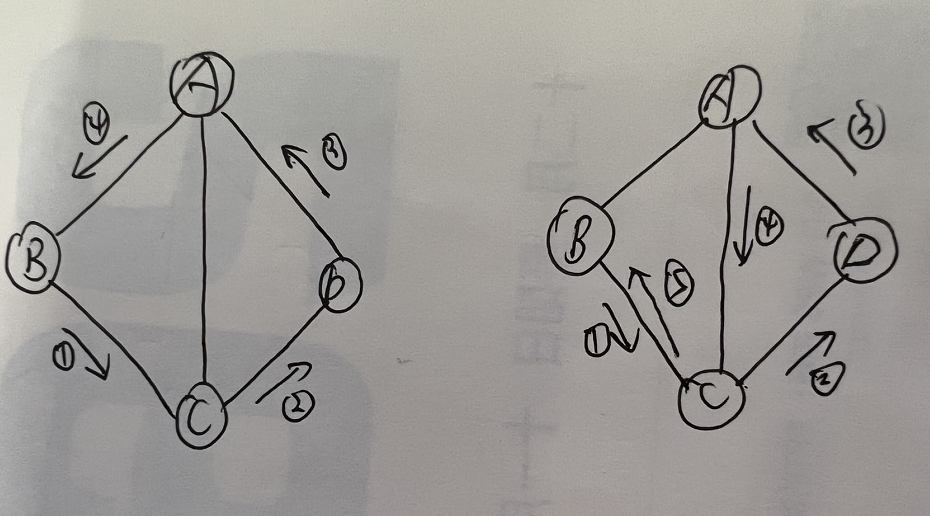
2. 有n个结点的无向完全图有$\frac{n*(n-1)}{2}$条边。

有向边

1. 若从顶点$v_i$到$v_j$的边有方向，则称这条边为有向边，也称为弧（Arc）。用有序对<$v_i$,$v_j$>来表示。
   1. $v_i$称为弧尾，$v_j$称为弧头。

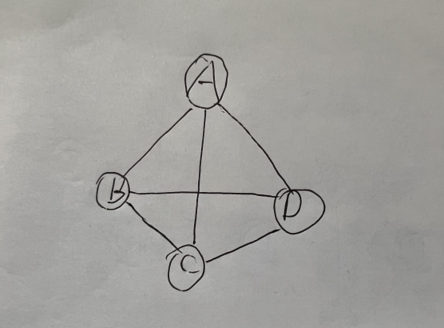
简单图

1. 不存在顶点到其自身的边，且同一条边不重复出现。
   1. 下图所示不是简单图。

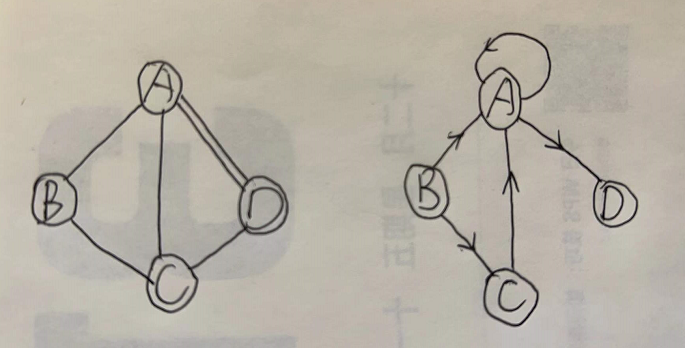
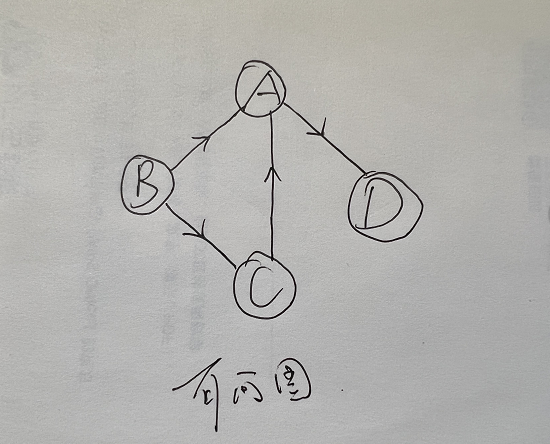
有向图

1. 如果图中任意两个顶点之间的边都是有向边，则称该图为有向图。
   1. 下图中，连接顶点A到D的有向边就是弧，A是弧尾，D是弧头，<A，D>表示弧。

有向完全图

1. 在有向图中，如果任意两个顶点之间都存在方向互为相反的两条弧，则该图为有向完全图。
2. 含有n个顶点的有向完全图有$n*(n-1)$条边。

稀疏图稠密图

1. 有很少条边或弧的图称为稀疏图，反之为稠密图。

带权的图

1. 与图的边或弧相关的数字。
2. 带权的图通常称为网。

子图

1. 假设有两个图G=(V,{E})和G'=(v',{E'})，如果$V'\subseteq V$，且$E' \subseteq E$，则称G‘为G的子图。

顶点与边的关系

1. 对于无向图G=(V,{E}):

   1. 如果边$(v,v') \in E$，则称顶点v和v'互为邻接点，即v和v'相邻接。
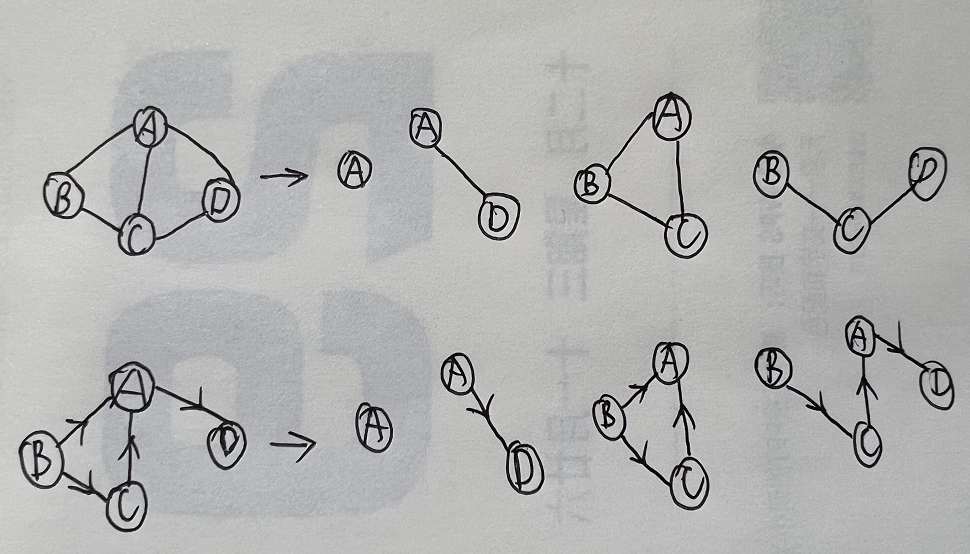
   2. 顶点v的度是和v相关联的边的数目，记为TD(v)。
   3. 边数就是各顶点度数和的一半，为$e=\frac{1}{2}\sum_{i=1}^nTD(v_i)$

2. 对于有向图G=(V,{E}):

   1. 如果弧$<v,v'> \in E$，则称顶点v邻接到顶点v'，顶点v'邻接自顶点v。弧<v,v'>和顶点v,v'相关联。
   2. 以顶点v为头的弧的数目称为v的入度ID(v)。以v为尾的弧的数目称为v的出度，记为OD(v)。顶点v的度为TD(v)=ID(v)+OD(v)。

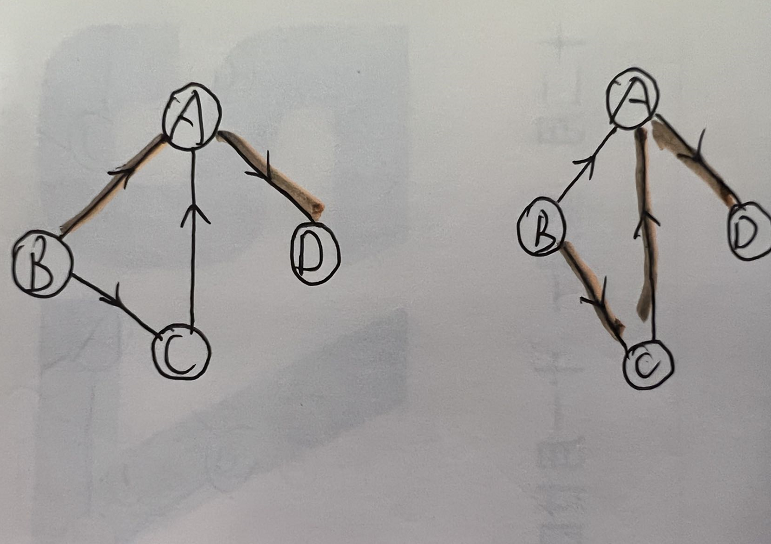
3. 无向图G=(V,{E})中从顶点v到顶点v'的路径是一个顶点序列($v=v_{i,0},v_{i,1},...,v_{i,m}=v'$)，其中，$v_{i,j-1},v_{i,j}\in E$，$1 \le j \le m$。
   如下图：

4. 如果是有向图，则路径也是相同的，顶点序列应满足$<v_{i,j-1}>,v_{i,j} \in E$，$1 \le j \le m$。

5. 路径的长度是路径上的边或弧的数目。
6. 第一个顶点到最后一个顶点相同的路径称为回路或环。
7. 序列中顶点不重复出现的路径称为简单路径。除了第一个顶点和最后一个顶点之外，其余顶点不重复出现的回路，称为简单回路或简单环。

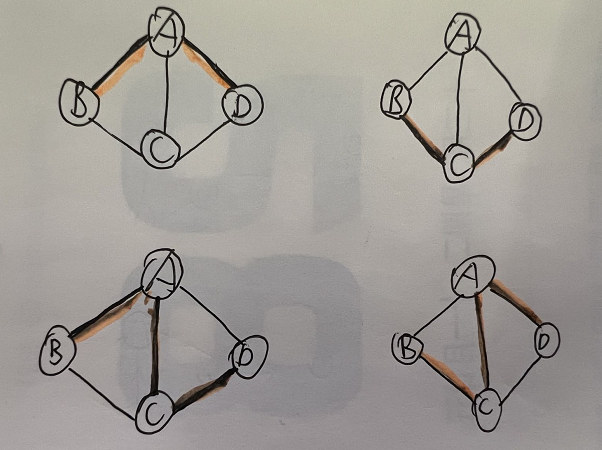
连通图

1. 在无向图中，如果从顶点v到顶点v'有路径，则称v和v'是连通的。
2. 对于图中任意两个顶点$v_i,v_j \in V$，$v_i$和$v_j$都是连通的，则称G是连通图。

连通分量

1. 无向图中的极大连通子图称为连通分量。
   1. 是子图
   2. 子图是连通的
   3. 连通子图含有极大顶点数
   4. 具有极大顶点数的连通子图包含依附于这些顶点的所有边
2. 在有向图G中，如果对于每一对$v_i,v_j \in V$，$v_i \ne v_j$，从$v_i$到$v_j$和从$v_j$到$v_i$都存在路径，则称G是强连通图。
   1. 有向图中的极大强连通子图称做有向图的强连通分量。

连通图生成树

1. 所谓的一个连通图的生成树是一个极小的连通子图，它含有图中全部的n个顶点，但只有足以构成一棵树的n-1条边。

有向树

1. 如果一个有向图恰有一个顶点的入度为0，其余顶点的入度均为1，则是一棵有向树。
2. 一个有向图的生成森林由若干棵有向树组成，含有图中全部顶点，但只有足以构成若干棵不相交的有向树的弧。