大话数据结构_赫夫曼树与应用

权

1. 树结点间的边相关的数叫权。

路径长度

1. 从树中一个结点到另一个结点之间的分支构成两个结点之间的路径，路径上的分支数目称做路径长度。
2. 树的路径长度就是从根到每一结点的路径长度之和。
3. 考虑到带权的结点：
   1. 结点的带权的路径长度为从该结点到树根之间的路径长度与结点上权的乘积。
   2. 树的带权路径长度为树中所有叶子结点的带权路径长度之和。
   3. 将带权路径长度WPL最小的二叉树称做赫夫曼树。

赫夫曼树的构造

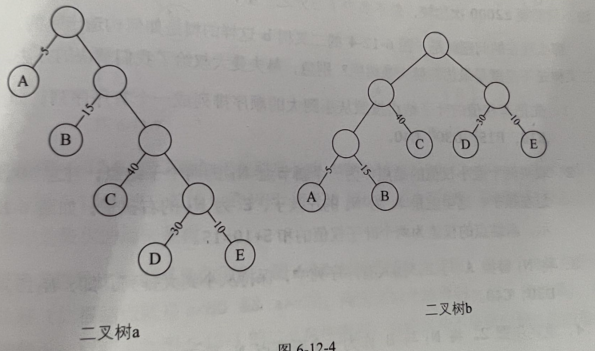
1. 先把有权值的叶子结点按照从小到大的顺序排列成一个有序序列
   即A5,E10,B15,D30,C40
2. 取头两个最小权值的结点作为一个新结点N_1的两个子结点，注意相对较小的是左孩子
   1. 即A为N_1的左孩子，E为N_1的右孩子
   2. 新结点的权值为两个叶子结点的权值的和
3. 将N_1替换A与E，插入有序序列中，保持从小到大排列
   即N_1 15,B15,D30,C40
4. 重复步骤2，将N_1与B作为一个新节点N_2的两个子结点。
5. 重复如上步骤，完成赫夫曼树的构造。

赫夫曼编码

1. 一般地，将需要编码的字符集为d_1,d_2,...,d_n，各个字符在电文中出现的次数或频率集合为w_1,w_2,...,w_n，以d_1,d_2,...,d_n作为叶子结点，以w_1,w_2,...,w_n作为相应叶子结点的权值来构造一棵赫夫曼树。
2. 规定赫夫曼树的左分支代表0，右分支代表1，则从根结点到叶子结点所经过的路径分支组成的0和1的序列便为该结点对应字符的编码，这就是赫夫曼编码。
   1. 完成赫夫曼树的构造后，将权值左分支改为0，右分支改为1。