大话数据结构_二叉树

定义

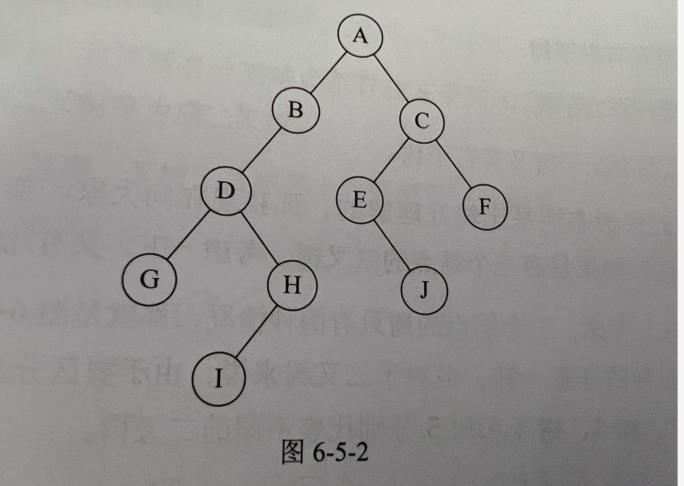
• 二叉树是n个结点的有限集合，该集合或者为空集（空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成

特点

• 每个结点最多有两棵子树，所以，二叉树中不存在度大于2的结点
• 左子树和右子树是有序的，次序不能任意颠倒
• 即使树种某一结点只有一棵子树，也要区分他是左子树还是右子树

二叉树的基本形态

• 空二叉树
• 只有一个根结点
• 根结点只有左子树
• 根结点只有右子树
• 根结点既有左子树又有右子树

特殊的二叉树

斜树

• 所有结点都在左子树上的二叉树叫左斜树，所有结点都在右子树上的二叉树叫做右斜树

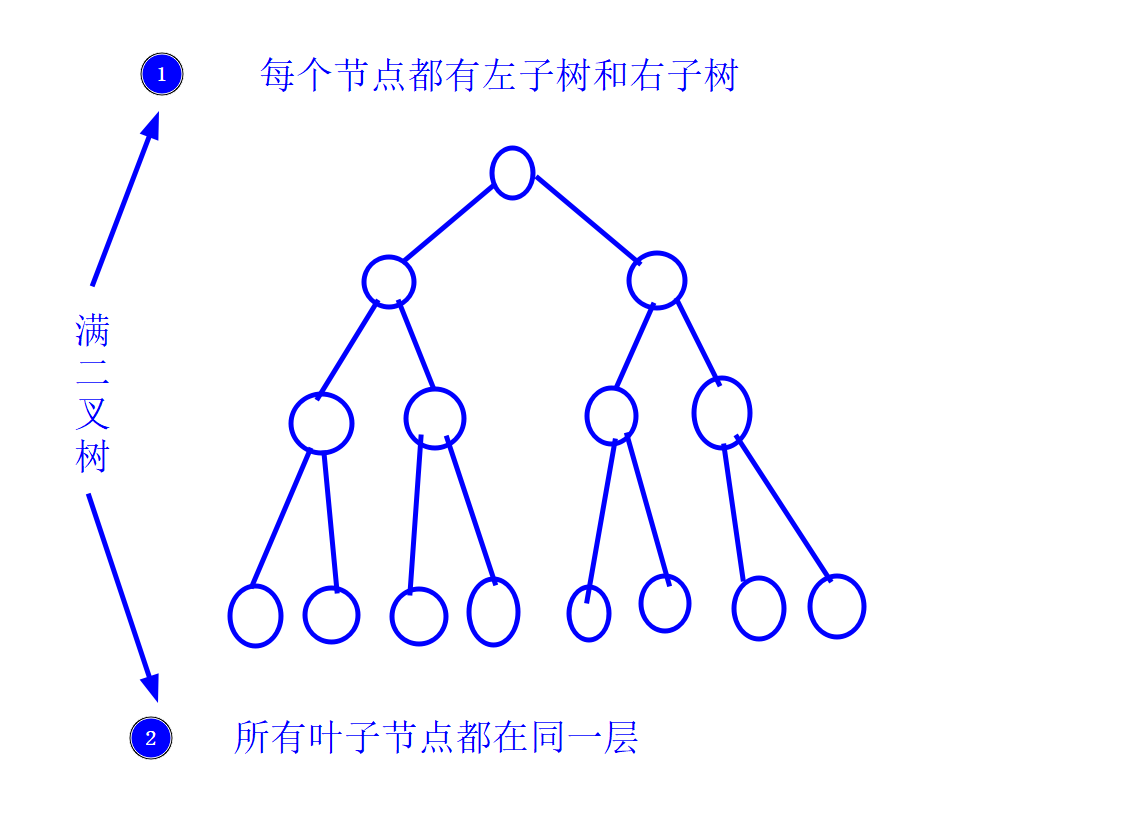
满二叉树

• 在一棵二叉树中，如果所有的分支结点，都存在左子树和右子树，并且，所有的叶子结点都在一层上，这样的二叉树，称为满二叉树
• 叶子结点只能出现在最下一层
• 非叶子结点的度，一定是2
• 在同样深度的二叉树中，满二叉树的结点个数最多，叶子数也最多

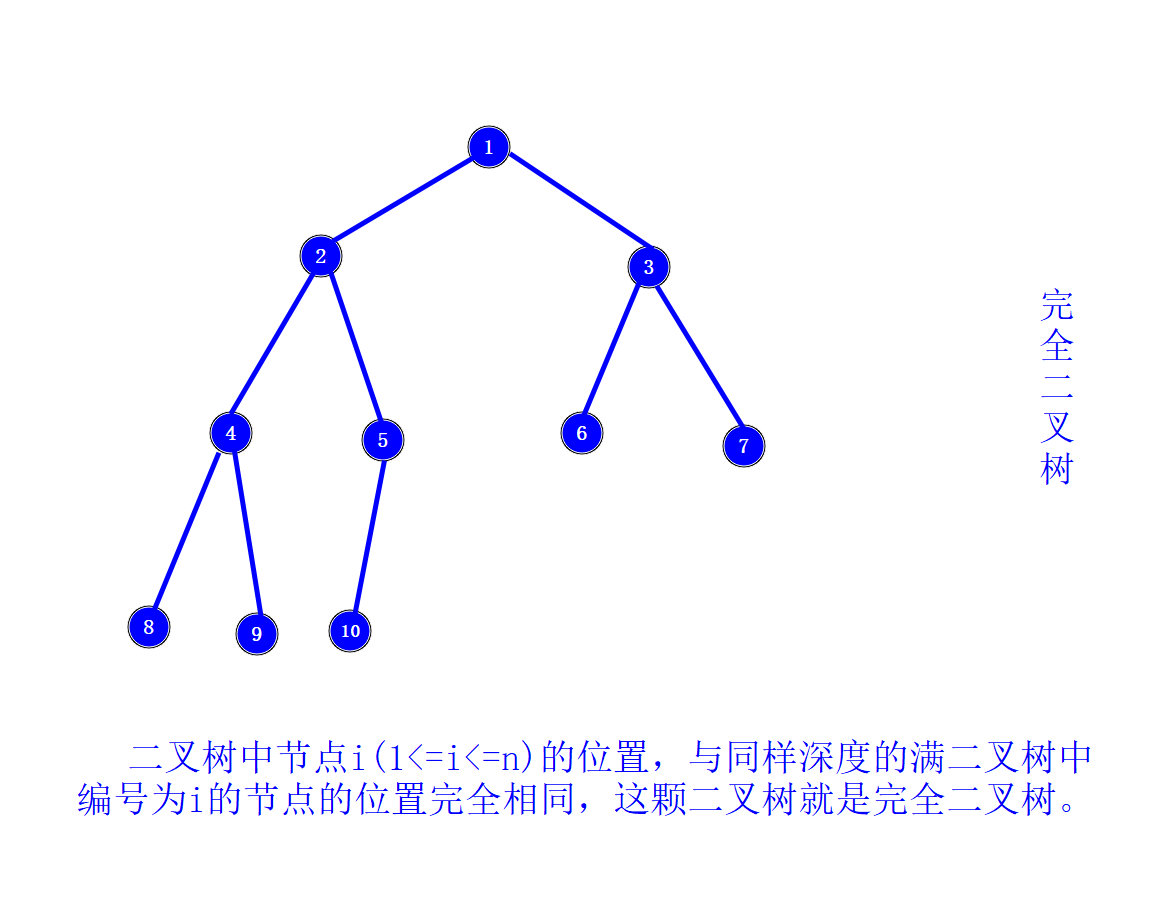
完全二叉树

• 对一棵具有n个结点的二叉树按层序编号，如果编号为i(1\leq i \leq n)的结点与同样深度的满二叉树中，编号为i的结点，在二叉树中位置完全相同，则这棵二叉树，称为完全二叉树
• 满二叉树一定是一棵完全二叉树，而完全二叉树不一定是满的
• 叶子结点只能出现在最下两层
• 最下层的叶子，一定集中在坐部连续位置
• 倒数第二层，如果有叶子结点，一定集中在右部连续位置
• 如果结点度为1，则该结点只有左子树，不存在有右子树的情况
• 同样结点的二叉树，完全二叉树的深度最小

二叉树的性质

• 在二叉树的第i层上，至多右2^{i-1}个结点（i\geq1）
• 深度为k的二叉树，至多有2^k-1个结点（k\geq1）
• 对任何一棵二叉树T，如果其终端结点数为n_0，度为2的结点数为n_2,则有：n_0 = n_2 + 1
• 具有n个结点的完全二叉树，深度为\lfloor log_2n \rfloor + 1。(其中，\lfloor x \rfloor表示不大于x的最大整数)
• 如果对一棵有n个结点的完全二叉树（其深度为\lfloor log_2n \rfloor + 1）的结点按照层序编号(从第1层到第\lfloor log_2n \rfloor + 1层，每层都从左到右),对任一结点i（1\leq i \leq n），有：
  1. 如果i = 1,则结点i是二叉树的根，无双亲；如果i>2，则其双亲结点是\lfloor i/2 \rfloor
  2. 如果2i > n，则结点i无左孩子（结点i为叶子结点）；否则其左孩子是结点2i
  3. 如果2i+1>n，则结点i无右孩子；否则其右孩子是2i+1